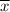по векторам имеет вид: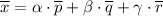
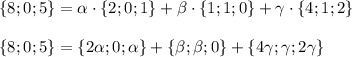
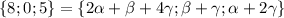
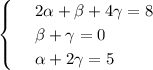
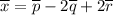
Випишемо координати початку O і кінця A вектора a:
O(0;0), A(1;3).
Обчислимо координати вектора a як різницю координат кінця A(1;3) та початку O(0;0):
A(1-0;3-0)=(1;3).
Пошаговое объяснение:
Обчислимо довжину (модуль) вектора a(1;3):
довжина вектора
Такі ж операції проводимо для вектора с:
O(0;0), C(3;1).
Координати вектора c знаходимо через різницю координат кінця C(3;1) та початку O(0;0):
c(3-0;1-0)=(3;1).
Через корінь квадратний з суми квадратів координат знаходимо довжину (модуль) вектора c(3;1):
модуль вектора
Скалярний добуток векторів a(1;3) і c(3;1):
a•c=1•3+3•1=6.
х-3=14
х=14+3
х=17