Как называется заболевание когда на коже появляются маленькие круги, а в них ещё что-то? нужно! видела - id539137720210309 от Novaya22 09.03.2021 09:48

Question

Математика: Как называется заболевание когда на коже появляются маленькие круги, а в них ещё что-то? нужно! видела множество картинок, но заболевание не запомнила (

Novaya22 · Accepted Answer

Вектор нормали M₁M₂ = {-10 - (-5); 9 - 5; 6 - 3} = {-5; 4; 3}.

Заданная нам плоскость, перпендикулярная искомой имеет вектор нормали 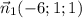$\vec n_1(-6;1;1)$ . Поскольку точки M₁ и М₂ принадлежат обеим плоскостям, а плоскости взаимно перпендикулярны, то

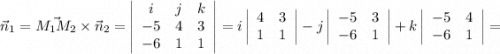
$\vec n_1=\vec{M_1M_2}\times \vec n_2=\left|\begin{array}{ccc}i&j&k\\-5&4&3\\-6&1&1\end{array}\right|=i\left|\begin{array}{ccc}4&3\\1&1\end{array}\right|-j\left|\begin{array}{ccc}-5&3\\-6&1\end{array}\right|+k\left|\begin{array}{ccc}-5&4\\-6&1\end{array}\right|=$

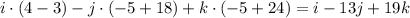
$i\cdot(4-3)-j\cdot(-5+18)+k\cdot(-5+24)=i-13j+19k$

Вектор нормали 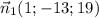$\vec n_1(1;-13;19)$ , т.к. точка 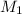M_1 принадлежит искомой плоскости, то её координаты должны удовлетворять этой плоскости, т.е. -5 - 13 * 5 + 19 * 3 + D= 0 откуда D = 13.

Итого получаем уравнение плоскости x - 13y + 19z + 13 = 0, где значения B, C, D соответственно равны (-13), 19, 13

Как называется заболевание когда на коже появляются маленькие круги, а в них ещё что-то? нужно! видела множество картинок, но заболевание не запомнила (

MOGZ ответил