y=3·x³-x и y=2x
Определим пределы интегрирования (точки пересечения графиков):
2х = 3·x³-x
3·x³-3х = 0
3х(х² - 1)= 0
х₁ = 0, х₂ = -1, х₃ = +1
На интервале от -1 до 0 3·x³-x > 2х
На интервале от 0 до +1 3·x³-x < 2х
1) Интегрируем в пределах от -1 до 0 следующее выражение
3·x³-x -2х = 3x³-3x = 3(x³-x)
3∫(x³-х)dx = 3(x⁴/4 - x²/2).
Подставим верхний и нижний пределы:
3/4 · 0⁴ - 3/2 ·0² - 3/4 (-1)⁴ + 3/2 (-1)² = 3/2 - 3/4 = 3/4 = 0,75
2) Интегрируем в пределах от 0 до +1 следующее выражение
2х - (3·x³-x) = -3x³+3x = 3(-x³+x)
3∫(-x³+x)dx = 3(-x⁴/4 + x²/2).
Подставим верхний и нижний пределы:
3(-1⁴/4 + 1²/2) - 3(-0⁴/4 + 0²/2)= -3/4 + 3/2 = 3/4 = 0,75
Сложим результаты интегрирования 1) и 2)
S = 0.75 +0.75 = 1.5
Пошаговое объяснение:
1. 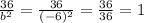
2. -1,3-(2,8-3,1)= -1,3-2,8+3,1= -4,1+3,1= -1
3. Собственная скорость лодки v₁ = m км/час, v₂ = n км/час. Тогда лодка плывёт против течения со скоростью
v = v₁ - v₂ = v₁ = m км/час - n км/час = (m - n) км/час
За 3,5 часа против течения лодка проплывёт расстояние
S=3,5 час · (m - n) км/час = 3,5 · (m - n) км
Нужное выражение S = 3,5 · (m - n) км
4.
а) 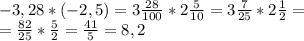
б) 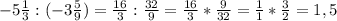
5. 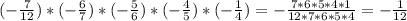
6. 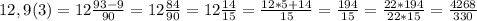
В тесте ошибка, так как 4267/330=12,9(30).
7. -1,3·(7+4·x)-11= -4,5
-1,3·7+(-1,3)·4·x= -4,5+11
-9,1-5,2·x=6,5
-5,2·x=6,5+9,1
-5,2·x=15,6
x= 15,6 : (-5,2)
x= - 3
8.
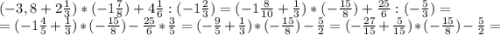
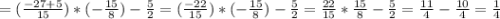

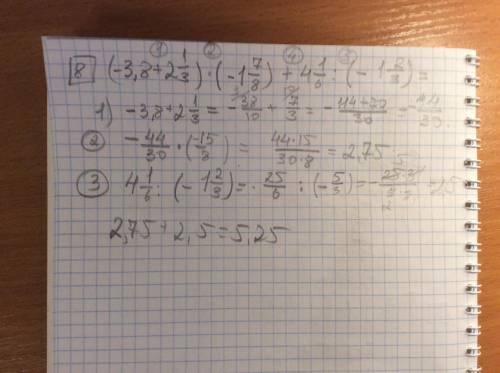
0,9
3,2
12,0
9,6