1) 81х² + 72х + 16 = 0
D = b² - 4ac = 72² - 4 · 81 · 16 = 5184 - 5184 = 0
Так как дискриминат равен 0, то уравнение имеет только один корень
х = (-72)/(2·81) = -72/162 = -4/9 (сократили на 18)
ответ: (-4/9).
2) 9х² - 12х + 4 = 0
D = b² - 4ac = (-12)² - 4 · 9 · 4 = 144 - 144 = 0
Так как дискриминант равен 0, то уравнение имеет только один корень
х = 12/(2·9) = 12/18 = 2/3 (сократили на 6)
ответ: 2/3.
3) 121у² - 110у + 25 = 0
D = b² - 4ac = (-110)² - 4 · 121 · 25 = 12100 - 12100 = 0
Так как дискриминант равен 0, то уравнение имеет только один корень
у = 110/(2·121) = 110/242 = 5/11 (сократили на 22)
ответ: 5/11.
4) 36у² + 12у + 1 = 0
D = b² - 4ac = 12² - 4 · 36 · 1 = 144 - 144 = 0
Так как дискриминант равен 0, то уравнение имеет только один корень
у = (-12)/(2·36) = -12/72 = -1/6 (сократили на 12)
ответ: (-1/6).
На обратную дорогу он потратил на 5 минут больше
1 ч. 5 мин. =13/12 ч.
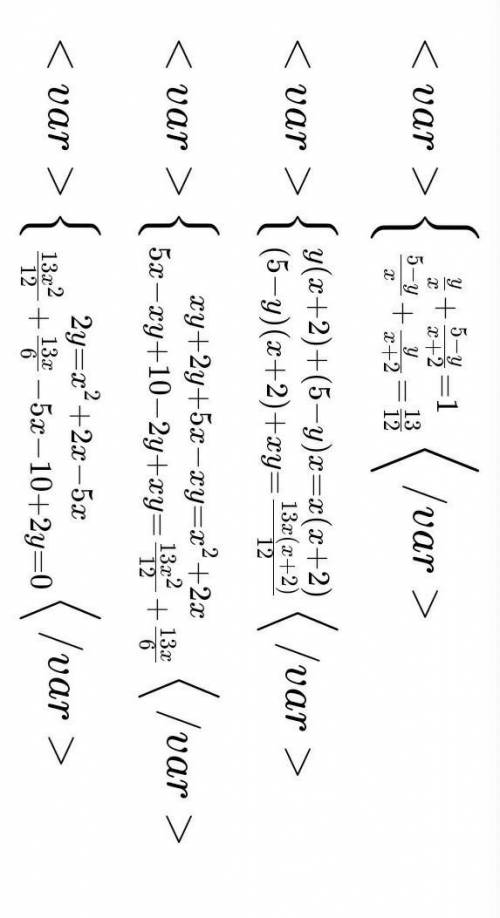
Пусть х км/ч - скорость на подъёме, тогда скорость на спуске - (х+2) км/ч. Пусть у км - расстояние от станции до вершины горы, тогда расстояние от вершины горы до озера - (5-у) км. На дорогу от станции до озера рыболов затратил у/x+(5-y)/(x+2) или 1 час; на обратную дорогу - (5-у)/x + у/(х+2) или 1,1 часа. Составим и решим систему уравнений: (фото)
По теореме Виета корнями уравнения
var > x2 - 2, 8.x - 4, 8 = 0 < /var >
являются 4 и -1,2. Так как скорость не может быть отрицательным числом, получаем, что скорость на подъёме была равна 4 км/ч, а на спуске 4+2=6 км/ч.
Путь от станции до вершины (4 2- 3*4)/2=2 км, от вершины до озера 5-2=3 км.
ответ: скорость на подъёме 4 км/ч, скорость на спуске 6 км/ч.


б) 4,5,6,7,8,9,10,11,12.
в) 1,2,3,4,5,6,7,8,9.
г) то же самое что и б).
д) то же самое что и в).
е) то же самое что б) и г).