1) первоначально x шаров. Чёрных шаров было 0,65x. После того, как Маша достала 6 чёрных шаров, всего осталось x-6 шаров, чёрных стало 0,65x-6, что составляет 50% или 0,5 от общего количества оставшихся шаров.
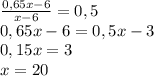
ответ: первоначально в ящике было 20 шаров
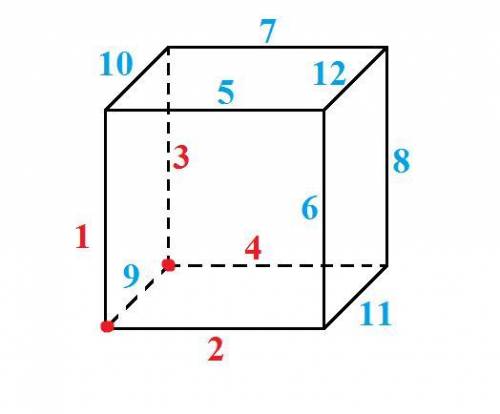
2) См. рис. От каждой вершины начинает гореть 3 ребра. Сначала одновременно сгорят рёбра 1, 2, 3 и 4 (4 минуты), потом рёбра 5, 6, 7 и 8 (ещё 4 минуты). Рёбра 9, 10, 11 сгорят, пока будут гореть рёбра 1-8. Последним сгорит ребро 12, на это уйдёт ещё 2 минуты (т.к. оно будет гореть с двух концов). Весь кубик сгорит за 4+4+2 = 10 минут.
3) Было x сиклей
1 обмен - 5 сиклей на 3 галеона и 1 кнат (x-5 сиклей, 3 галеона, 1 кнат)
2 обмен - 5 сиклей на 3 галеона и 1 кнат (x-10 сиклей, 6 галеонов, 2 кната)
3 обмен - 2 галеона на 3 сикля и 1 кнат (x-7 сиклей, 4 галеона, 3 кната).
4 обмен - 2 галеона на 3 сикля и 1 кнат (x-4 сиклей, 2 галеона, 4 кната).
5 обмен - 2 галеона на 3 сикля и 1 кнат (x-1 сиклей, 0 галеонов, 5 кнатов).
Очевидно, что повторив обмены с 1 по 5 десять раз, у Гарри на руках будет 50 кнатов и 0 галеонов. При этом количество сиклей уменьшается на 1 за обмены с 1 по 5. Значит, количество сиклей уменьшится на 10.
Пошаговое объяснение:
1*(1+0.01x)*(1+0.01x)=1.69
еренесём правую часть уравнения в
левую часть уравнения со знаком минус.
Уравнение превратится из
$$\left(\frac{x}{100} + 1\right) \left(\frac{x}{100} + 1\right) = \frac{169}{100}$$
в
$$\left(\frac{x}{100} + 1\right) \left(\frac{x}{100} + 1\right) - \frac{169}{100} = 0$$
Раскроем выражение в уравнении
$$\left(\frac{x}{100} + 1\right) \left(\frac{x}{100} + 1\right) - \frac{169}{100} = 0$$
Получаем квадратное уравнение
$$\frac{x^{2}}{10000} + \frac{x}{50} - \frac{69}{100} = 0$$
Это уравнение вида
a*x^2 + b*x + c = 0
Квадратное уравнение можно решить
с дискриминанта.
Корни квадратного уравнения:
$$x_{1} = \frac{\sqrt{D} - b}{2 a}$$
$$x_{2} = \frac{- \sqrt{D} - b}{2 a}$$
где D = b^2 - 4*a*c - это дискриминант.
Т.к.
$$a = \frac{1}{10000}$$
$$b = \frac{1}{50}$$
$$c = - \frac{69}{100}$$
, то
D = b^2 - 4 * a * c =
(1/50)^2 - 4 * (1/10000) * (-69/100) = 169/250000
Т.к. D > 0, то уравнение имеет два корня.
x1 = (-b + sqrt(D)) / (2*a)
x2 = (-b - sqrt(D)) / (2*a)
или
$$x_{1} = 30$$
$$x_{2} = -230$$
проверка:
9*2=18
9-2=7