(m+2) x²+(m+2)*x+m-2<0
1) Если m=-2, то у=-4
2) Если m≠-2, получаем квадратичную функцию относительно х. Если первый коэффициент этой функции больше нуля, а дискриминант меньше нуля, то функция положительна при любом действительном значении х. Графически это означает, что парабола направлена ветвями вверх и не пересекается с осью ох.
m+2>0 ⇒m>-2, т.е. m∈(-2;+∞)
D(x)=(m+2)²-4(m²-4)<0 (D(x) -дискриминант относительно переменной х); m²+4m+4-4m²+16<0; -3m²+4m+20<0; 3m²-4m-20=0;
m=(2±√(4-60))/3=(2±8)/3; m=10/3; m=-2; решим неравенство
-3*(m-(10/3))(m+2)<0 методом интервалов.
-210/3
- + -
m∈(-∞;-2)∪(10/3;+∞)
С учетом m∈(-2;+∞) выходим на ответ А) m>10/3
m>3 1/3
Пошаговое объяснение:
4.71
2x + Iax-5I = 0
запишем в виде Iax-5I = -2x
теперь получим первое и главное условие для решения х<0
и вот раскроем модуль
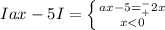
при любом раскладе 5/(а±2) должно быть <0, т.е при а> 2 решений нет
теперь рассмотрим первую строчку
ax-5 = 2x ⇒ х = 5/(а-2), при этом x<0, значит а-2<0, a<2
это мы нашли один интервал
теперь
ax-5 = 2x ⇒ х = 5/а+2, при этом x<0, значит а+2<0, a < -2
и теперь еще условие а≠ 2, т.к. знаменатель не может быть равен 0, т.е при а = 0 решений нет
ну вот, в общем-то и всё
теперь нанесем все точки а и значения х на числовую ось и получим решение
a < -2 х = 5/а±2
-2 ≤a <2 х = 5/(а-2)
a ≥ 2 нет решения
(не совсем сходится с ответом, но в ответе есть ошибка. при a = -2
х не может быть равен 5/а+2, т.к. знаменатель будет 0
1)54+37=91
2)91:13=7
3)78:6=13
4)13+7=20