Добрые люди умоляю 1)периметр треугольника авс = 24 см. длина стороны ав состовляет 35%,а длина стороны вс-25% периметра треугольниканайдите длину стороны ас 2)в селе 620 домов.в 80% домов есть собака, в 50%-кошка. в скольких домах есть кошка и собака?
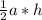
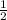 a · b · sin γ
a · b · sin γ 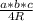
40% = 0,4
24 * 0,4 = 9,6 (см) - сторона АС.
ответ: 9,6 см.
2) 80% + 50% - 100% = 30% - домов, где есть кошка и собака.
30% = 0,3
620 * 0,3 = 186 (д.)
ответ: в 186 домах есть кошка и собака.