S = a * b
1 сп.
Пусть х см - 1 сторона, тогда 2 сторона будет равна х - 44 см. По условию задачи площадь равна 675см².
Составим уравнение :
675 = х * ( x - 44 )
675 = x² - 44x
x² - 44x - 675 = 0
По теореме, противоположной теореме Виета:
x1 = 22 + √1159
x2 = 22 - √1159
2 сп.
Пусть х см - 2 сторона, тогда 1 сторона будет равна х + 44 см. По условию задачи площадь равна 675 см².
Составим уравнение:
675 = х * ( х + 44 )
675 = х² + 44х
х² + 44х - 675 = 0
По теореме, противоположной теореме Виета:
х1 = -22 + √1159
х2 = -22 - √1159 - корень отрицательный, что не может быть ( сторона не может быть отрицательной ), значит его мы не берём.
ответ: -22 + √1159 см
Для построения треугольника нужно взять 3 точки. Эти точки не могут лежать на одной прямой. Чтобы построить треугольник, нужно брать две точки на одной прямой и одну точку на другой.
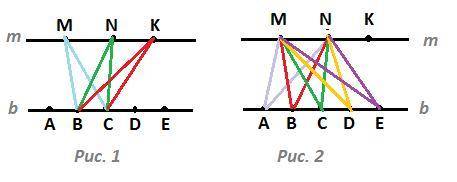
Рис. 1. На прямой b отмечено 5 точек. Первую точку можно выбрать вторую точку можно выбрать из 4 оставшихся. Так как для треугольника не важно, в каком порядке выбраны вершины, пары точек А,В и В,А равнозначны. Тогда всего вариантов выбрать 2 точки из 5
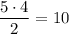
Либо по формуле сочетаний 2 из 5
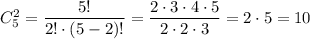
Для каждой пары точек на прямой b, например, для пары В,С, можно выбрать одну из трёх точек, отмеченных на прямой m. Получится 3 треугольника : ΔBCM, ΔBCN, ΔBCK.
Всего треугольников из 2 точек на прямой b и одной точки на прямой m можно построить 10 · 3 = 30.
Рис. 2. На прямой m отмечено 3 точки. Выбрать две из них можно тремя или M,K или N,K. Для каждой пары можно подобрать одну из пяти точек, отмеченных на прямой b. На рисунке показаны треугольники для пары точек M,N.
Всего треугольников из двух точек на прямой m и одной точки на прямой b можно построить 3 · 5 = 15.
30 + 15 = 45
ответ : 45 треугольников
kx = 3
0,2к=3
к=3/0,2=15
15х=-1
х=-1/15