Длина прямоугольника равна 32см на сколько квадратных сантиметров уменьшится площадь этого прямоугольника если его ширину
уменьшить на 5 см.
Пошаговое объяснение:
Решение задачи.
1. Обозначим через х первоначальную ширину прямоугольника.
2. Рассчитаем первоначальную площадь прямоугольника.
32см * х см = 32х см^2.
3. Найдем новую ширину прямоугольника.
х - 5 см.
4. Вычислим новую площадь прямоугольника.
32 см * (х - 5) см = 32х - 160 см^2
5. Определим, на сколько квадратных сантиметров уменьшится площадь этого прямоугольника.
32х см^2 - (32x - 160) см^2 = 160 см^2.
ответ. Площадь прямоугольника уменьшится на 160 квадратных сантиметров.
AB=15 см, BC=10 см, CD=9 см, DA=22 см
Пошаговое объяснение:
Дано:
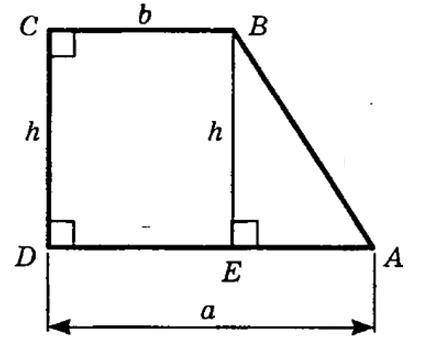
ABCD - трапеция (см. рисунок)
∠B=∠D=90°
Sтрапеция = 144 см²
h=CD=BE=9 см
a=b+12 см
Найти: AB, BC, CD, DA.
Решение.
Площадь трапеции определяется через основания и высоте по формуле:
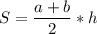
Учитывая заданные значения, имеем
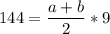
a+b=2·(144:9)
b+12+b=32
2·b=20
BC=b=10 см
Тогда DA=a=b+12 см = 10 см + 12 см= 22 см.
Известно: h=CD=BE=9 см.
Остается найти AB.
Так как треугольник ABE прямоугольный, то по теореме Пифагора
AB²=BE²+EA².
Но BE=9 см, EA=DA-BC= 22 см - 10 см = 12 см. Тогда
AB²=9²+12² = 81+144=225=15² или
AB=15 см.
ответ: AB=15 см, BC=10 см, CD=9 см, DA=22 см.
4х+у=23
у=23-4х
3(х+2(23-4х))-23+4х=27
3(х+46-8х)-23+4х=27
3х+138-24х-23+4х=27
-17х=27-115
-17х=-88
х=88:17
х=5 3\17
у=23-4х=23-4*88/17=23-692\17=23-40 12/17=-17 12\17