 — попарно независимые случайные величины, следовательно для нахождение дисперсий их произведения достаточно воспользоваться формулой:
— попарно независимые случайные величины, следовательно для нахождение дисперсий их произведения достаточно воспользоваться формулой:![D[X_{a}X_{b}] = D[X_{a}]D[X_{b}]+D[X_{a}](M[X_{b}])^{2}+D[X_{b}](M[X_{a}])^2](/tpl/images/0508/1988/7c356.png)
![D[X_1X_2]](/tpl/images/0508/1988/4f2b9.png) мы должны убедится, что
мы должны убедится, что 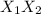 независима от
независима от 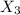 и
и 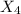 . В этом легко убедиться исходя из условия попарной независимости: произведение двух из трех попарно независимых величин независимо от оставшейся.
. В этом легко убедиться исходя из условия попарной независимости: произведение двух из трех попарно независимых величин независимо от оставшейся. ![M[X_aX_b]=M[X_a]M[X_b]](/tpl/images/0508/1988/381c5.png)
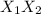 :
:![D[X_1X_2]=D[X_1]D[X_2]+D[X_1](M[X_2])^{2}+D[X_2](M[X_1])^{2}=2+4+8=14](/tpl/images/0508/1988/1de15.png)
![M[X_1X_2]=M[X_1]M[X_2]=-2\cdot{-2}=4](/tpl/images/0508/1988/3dbe0.png)
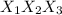 :
:![D[X_1X_2X_3] = D[X_1X_2]D[X_3]+D[X_1X_2](M[X_3])^{2}+D[X_3](M[X_1X_2])^{2}=14\cdot3+14\cdot4+3\cdot16=42+56+48=146](/tpl/images/0508/1988/0a453.png)
![M[X_1X_2X_3]=M[X_1X_2]M[X_3]=-2\cdot4=-8](/tpl/images/0508/1988/12b0c.png)
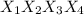 :
:![D[X_1X_2X_3X_4]=D[X_1X_2X_3]D[X_4]+D[X_1X_2X_3](M[X_4])^{2}+D[X_4](M[X_1X_2X_3])^{2}=146\cdot4+146\cdot4+4\cdot64=584+584+256=1424](/tpl/images/0508/1988/207de.png)
![M[X_1X_2X_3X_4]=M[X_1X_2X_3]M[X_4]=-8\cdot{-2}=16](/tpl/images/0508/1988/75b22.png)
В древние времена люди полагали, что Солнце, перемещаясь относительно звезд, обходит нашу планету по кругу в течение одного года, Земля же будто бы неподвижна и находится в центре Вселенной. Такая система получила название геоцентрической . Новый этап в развитии астрономии начинается с опубликования в 1543г. книги Н. Коперника «О вращении небесных тел», в которой (Гелиос- «солнце») система мира, отражающая действительное строение Солнечной системы. Согласно теории Н. Коперника центром мира является Солнце, вокруг которого движутся шарообразная Земля и все подобные ей планеты и притом в одном направлении, вращаясь каждая относительно одного из своих диаметров, и что только Луна вращается вокруг Земли, являясь его постоянным спутником, и вместе с последней движется вокруг Солнца, при этом примерно в одной и той же плоскости
Для определения положения тех или иных светил на небесной сфере необходимо иметь «опорные» точки и линии. И здесь, прежде всего, используется отвесная линия, направление которой совпадает с направлением силы тяжести. Продолженная вверх и вниз эта линия пересекает небесную сферу в точках Z и Z ’, называемых соответственно зенитом и надиром.
Большой круг небесной сферы, плоскость которого перпендикулярна линии ZZ ’, называется математическим или истинным горизонтом . Диаметр РР’, вокруг которого вращается в своем видимом движении небесная сфера (это ее вращение является отражением вращения Земли), и называется осью мира: она пересекает поверхность небесной сферы в двух точках - северном Р и южном Р’ полюсах мира. Большой круг небесной сферы QLQ ’ F , плоскость которого перпендикулярна оси мира РР’, является небесным экватором ; он делит небесную сферу на северное и южное полушария. Вращающаяся вокруг своей оси Земля движется вокруг Солнца по пути, лежащему в плоскости земной орбиты VLWF .