Используем свойство: сумма цифр числа дает один и тот же остаток при делении на 9, что и само число.
И правда: пусть число имеет вид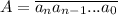 
. Тогда 
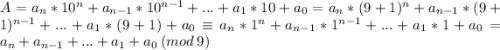- т.е. число сравнимо по модулю 9 с суммой своих цифр. Из этого и следует необходимое утверждение.
А значит применяя к числу 2019! приведенную в условии операцию, мы будем получать на каждом шаге числа, дающие тот же остаток при делении на 9, что и 2019!. Т.к. 2019>9, то 2019! делится на 9.
Из однозначных чисел на 9 делятся только 0 и 9. Т.к. сумма цифр числа равна 0 только у числа 0, то последним осталось число 9.
х-640=921:3
х-640=307
х=307+640
х=947
х:9=2007:9
х:9=223
х=223*9
х=2007
х*81=729:3
х*81=243
х=243:81
х=3