Если диагональ квадрата равна 20, то сторона квадрата: a = 20/√2 = 10√2.
Найдём диаметр цилиндра: d = 8•2 = 16.
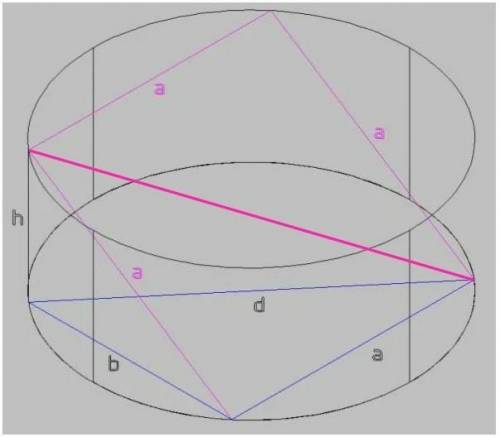
По условию плоскость квадрата АВСD не параллельна оси цилиндра. В этом случае центр квадрата совпадает с центром цилиндра.
На рисунке проекция квадрата на основание показана синим цветом.
b — проекция наклонной стороны квадрата на плоскость основания.
По теореме Пифагора: a² + b² = d² ;
b² = d² - a² = 16² - (10√2)² = 256 - 100•2 = 56;
b = √56 = 2√14.
И снова по теореме Пифагора, но уже для вертикально расположенного прямоугольного треугольника:
h² + b² = a² ;
h² = a² - b² = (10√2)² - (2√14)² = 200 - 56 = 144;
h = √144 = 12.
Тогда а * х = 18 см²
Тогда 2а + 2х=18 см
В первом утверждении где а * х = 18 см²
а=1,2,3.
х=18,9,6.
Подставляем а и х во второе утверждение где 2а + 2х=18 см
Первый случай: 2 * 1 + 2 * 18 = 38 ,а надо 18
Второй случай: 2 * 2 + 9 * 2 = 22 ,а надо 18
Третий случай: 2 * 3 + 2 * 6 = 18
Третий случай подходит.
Значит стороны будут 3 см и 6 см.
ответ: стороны будут равны 3 см и 6 см.