Задание 1
Как нам известно, по теореме Виета сумма корней квадратного уравнения равна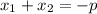 
, а их произведение: 
.
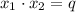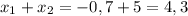. Следовательно 
.
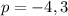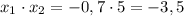. Следовательно 
.
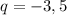Однако, в задании требуется составить квадратное уравнение с целыми коэффициентами. Значит, все показатели нужно умножить на 10. Итак, вот наше квадратное уравнение:
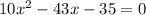
Задание 2
Как нам известно, по теореме Виета сумма корней квадратного уравнения равна 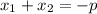, а их произведение: 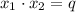. Это модификация стандартного квадратного уравнения. Поэтому 
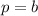, а 
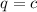. Так же мы знаем, что применение теоремы Виета возможно только в том случае, если 
(коэффициент перед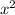 
) равен 1. Приступаем к вычислениям.
.
.
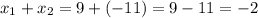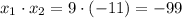Итак, вот наше квадратное уравнение:
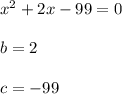
Задание 3
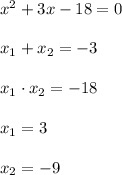
24*2 = 3 (a1+a3)
16 = a1 + a3
по свойству арифметической прогрессии, средний член равен среднему арифметическому двух соседних, тогда
а2 = (а1 + а3) / 2 = 16/2=8