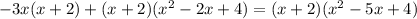
1.) 3,6 - 3(2,2x + 4)
1.1.) Сначала раскрываем скобки и перемножаем каждое слагаемое на множитель 3: 3,6 - 6,6x - 12
1.2.) Из известного уменьшаемого (3,6) вычитаем известное вычитаемое (12): 3,6 - 12 - 6,6x = - 8,4 - 6,6x
1.3.) ответ: - 8,4 - 6,6x
2.) 3,7 - 3,2(4a - 3) - (7a + 5,2)
2.1.) Сначала раскрываем первые скобки и перемножаем каждое слагаемое на множитель 3,2, и затем раскрываем вторые скобки: 3,7 - 12,8a - 9,6 - (7a + 5,2) = 3,7 - 12,8a - 9,6 - 7a - 5,2
2.2.) Следующим действием приводим подобные слагаемые (как в первом примере): 3,7 - 12,8a - 9,6 - 7a - 5,2 = - 11,1 - 19,8a
2.3.) ответ: - 11,1 - 19,8a
_ x^3 - 3x^2 - 6x + 8 |x + 2
x^3 + 2x^2
x^2 - 5x + 4
_ -5x^2 - 6x
-5x^2 - 10x
_ 4x + 8
4x + 8
0
x^2 - 5x + 4 - тут по т.Виетта легко найти корни
x1 + x2 = 5
x1 * x2 = 4
x1 = 1, x2 = 4
Итого, исходное выражение представляется в виде:
(x + 2)(x - 1)(x -4)