Покажем, что последняя цифра не может быть двойкой. Действительно, если это так, то пусть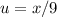 
. Тогда 
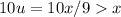, но поскольку эти числа отличаются лишь последней цифрой (и 2>0), то 
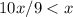, противоречие.
Это был один из начать рассуждение, которое, однако, вряд ли к чему либо приведет.
Рассмотрим другой подход. Заметим, что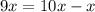 
. Пусть исходное число построено так: 
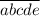. Пусть 
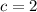. Тогда ![\overline{abced}=9\times \overline{abed}=\overline{abed0}-\overline{abed}\leq \overline{a[b-1]ed0}](/tpl/images/1428/2431/04d5d.png)
, противоречие. Аналогично доказывается для любой позиции двойки в числе, кроме второй слева. Идея состоит в том, что вычитаемое четырехзначное число достает таким образом до позиции, которая остается в числе, а значит, нарушает равенство. Остается лишь сделать так, чтобы эта позиция исчезала. Собственно, поставить двойку на вторую позицию
Теперь рассмотрим вычитание столбиком:
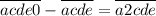, откуда ясно, что 
, 
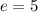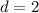или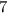 
, но два быть не может, поскольку у нас ровно одна двойка, 
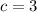или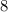 
, наконец 
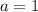или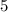 
.
Получаем два числа: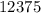 
и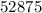 
.
√(x-y) = 10 - 3*√(x+y)
Подставляем в 1ое уравнение и получаем:
2*√(x+y) - 30 + 9*√(x+y) = 3
Приводим подобные и получаем что x+y = 9, откуда x=9-y
Подставляем вместо X во 2ое уравнение
√(9-2y) = 10 - 3*√9
И получаем что y = 4, а x = 5