в 3 номере под а):
показатели корней разные (12 и 6), мы можем получить одинаковые, умножив показатель 6 на 2, поэтому и подкоренное выражение домножаем на 2:
было: √6ой степени из 5⁵, стало: √12ой степени из 5¹⁰
то же самое в номере 3 под б):
показатели корней разные (квадратный корень из 3 и кубический корень из 9), мы можем получить одинаковые, домножив квадратный корень на 3 (чтобы получить 6) и кубический корень на 2 (чтобы получить 6), поэтому и подкоренные выражения домножаем на 2:
было: √2ой степени из 3, стало: √6ой степени из 3³ и второй множитель: было: √3ей степени из 9, стало: √6ой степени из 9²
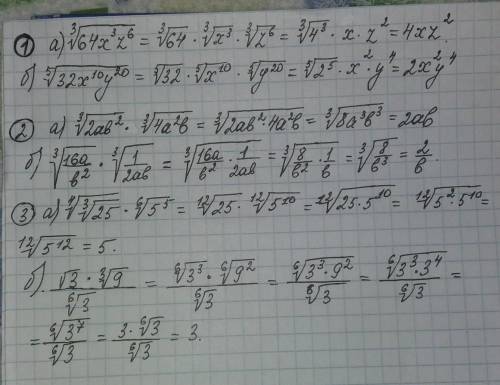
непрерывная случайная величина в результате испытания может принимать значения на некотором интервале. непрерывная случайная величина считается заданной, если известен вид ее функции распределения вероятностей или функции плотности вероятности.
функцией распределения вероятностей случайной величины называют функцию одной переменной f такую, что f(x)=p(x
свойства функции распределения.
1. для любого значения функции распределения заключены в промежутке .
2. ; .
3. является неубывающей функцией.
4. вероятность попадания случайной величины x в интервал [x1,x2) вычисляют по формуле p(x1≤x
вероятность того, что непрерывная случайная величина x примет конкретное значение a, равно нулю, то есть p(x=a)=0 для любого числа a.
7Х-вес семи пачек маргарина, а 4Х - вес 4 пачек маргарина соответственно. Запишем следующее равенство:
7Х+750=4Х+3000, переносим все слагаемые с Х влево, без Х - вправо
3Х=3000-750
3Х=2250
Х=2250/3
Х=750, следовательно 750 грамм вес одной пачки маргарина.