Пусть это число abcd Если оно делится на 36, то оно делится на 4 и на 9.Сумма его цифр 18, значит оно точно делится на 9. Чтобы число делилось на 4, нужно, чтобы две его последние цифры образовали число делящееся на 4.
т.к. 2000<abcd < 2400, то а=2, b может принимать значения 1, 2 или 3 .
Сумма b+c+d=18-2=16 и d- четное. Рассмотрим случаи
d=0, значит b+c=16, зная что b≤3, а 1≥с≥9, то подходящих вариантов нетd=2, значит b+c=16-2=14, зная что b≤3, а 1≥с≥9, то подходящих вариантов нетd=4, значит b+c=16-4=12, то подходит b=3 c=9,но 94:4.d=6, значит b+c=16-6=10. 1+9 (96 делится на 4), получаем 21962+8 (86 не делится на 4)3+7 (76 делится на 4), получаем 2376d=8, значит b+c=16-8=81+7 (78 не делится на 4)2+6 (68 делится на 4), получаем 22683+5 (58 не делится на 4)ответ: 2196 или 2268 или 2376
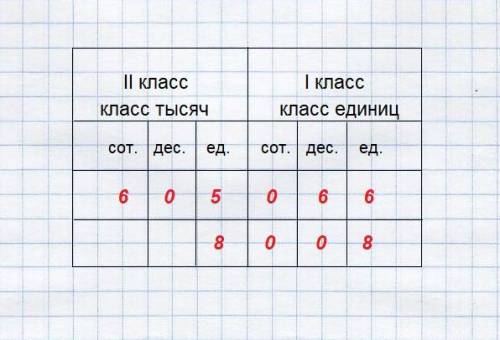
Таблица в приложении.
----------------------------------------
а) 605 066 - шестьсот пять тысяч шестьдесят шесть
содержит: 605 единиц II класса и 66 единиц I класса
сумма разрядных слагаемых: 600 000 + 5 000 + 60 + 6 = 605 066
605 066 - означает разряд сотен II класса
605 066 - означает разряд единиц II класса
605 066 - разряд десятков I класса
605 066 - разряд единиц I класса
б) 8 008 - восемь тысяч восемь
содержит: 8 единиц II класса и 8 единиц I класса
сумма разрядных слагаемых: 8 000 + 8 = 8 008
8 008 - разряд единиц II класса
8 008 - разряд единиц I класса