6
Пошаговое объяснение:
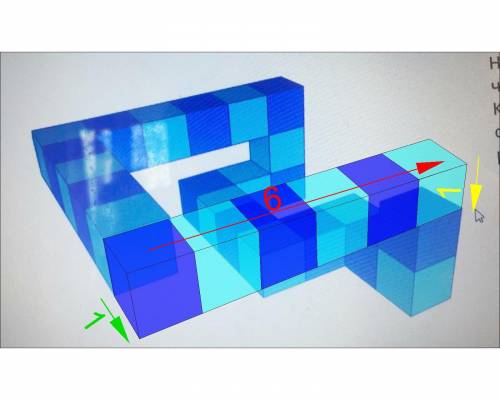
Для правильного решения задания нужно внимательно рассмотреть рисунок и поочерёдно просчитать смещение относительно начального кубика в трёх направлениях.
На первом рисунке показаны смещение вдоль оси z - жёлтым цветом, вдоль оси у - зелёным цветом, вдоль оси х - красным цветом.
Посчитаем, как сместилась конечная точка от начальной:
х: -3+3-6 = -6
у: 2+4-5 = 1
z: -2+3 = 1.
Значит нужно из конечной точки сместиться на:
-1 вдоль оси у,
+6 вдоль оси х,
-1 вдоль оси z.
На втором рисунке мы видим что смещение на -1 вдоль оси у и -1 вдоль оси z обеспечивается стыковкой горизонтальной полосы из 6 кубиков, которые дают смещение на +6 вдоль оси х.

1) уравнение вида y = kx + b: y = 5/4 * x + 3/4
2) прямая проходит через точки M1(0; 3/4) и M2(4; 23/4). Направляющий вектор a = {4-0; 23/4 - 3/4} = {4; 5}. Каноническое уравнение прямой: x/4 = (y - 3/4)/5
3) t = 1/sqrt(25+16) = 1/sqrt(41). Нормальное уравнение: 5*x/sqrt(41) - 4*y/sqrt(41) + 3/sqrt(41) = 0
4) прямая проходит через точки M1(0; 3/4) и M2(4; 23/4). Уравнение прямой, проходящей через две точки: x/4 = (y - 3/4)/5
5) C = 3. Поделим общее уравнение на -С = -1: -5x/3 +4y/3 - 1 = 0
Могу где-то ошибаться :)
261.97
31.10204
23.8
сделано и проверени