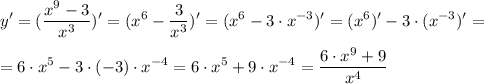Если каждую цифру двузначное число записать как однозначное число ты их сумма равна девяти если эти цифры поменять местами то получится число которое на шься три меньше первоначального числа найдите первоначальное число

👇

Увидеть ответ

Ответ:

larisavenzel

09.05.2023

Это число 81. Переставим цифры - будет 18. 81-18=63.

4,7(16 оценок)

Открыть все ответы

Ответ:

Anway2017

09.05.2023

1. Найдите значение производной функции в точке x₀:

a) y=(3·x-2)⁷, x₀=3

y'=((3·x-2)⁷)'=7·(3·x-2)⁶·(3·x-2)'=7·(3·x-2)⁶·3=21·(3·x-2)⁶

y'(3)=21·(3·3-2)⁶=21·7⁶=21·117649=2470629

б) y=(4-5·x)⁷, x₀=1

y'=((4-5·x)⁷)'=7·(4-5·x)⁶·(4-5·x)'=7·(4-5·x)⁶·(-5)= -35·(4-5·x)⁶

y'(1)= -35·(4-5·1)⁶= -35·(-1)⁶= -35·1= -35

в) y=(2·x+3)⁵, x₀=2

y'=((2·x+3)⁵)'=5·(2·x+3)⁴·(2·x+3)'=5·(2·x+3)⁴·2=10·(2·x+3)⁴

y'(2)=10·(2·2+3)⁴=10·7⁴=10·2401=24010

г) y=(5-3·x)⁷, x₀=1

y'=((5-3·x)⁷)'=7·(5-3·x)⁶·(5-3·x)'=7·(5-3·x)⁶·(-3)= -21·(5-3·x)⁶

y'(1)= -21·(5-3·1)⁶= -21·2⁶= -21·64= -1344

2. Вычислить скорость изменения функции в точке x₀ (скорость изменения равносильно производная первого порядка):

a) y=(2x+1)⁵, x₀= -1

y'=((2·x+1)⁵)'=5·(2·x+1)⁴·(2·x+1)'=5·(2·x+1)⁴·2=10·(2·x+1)⁴

y'(-1)=10·(2·(-1)+1)⁴=10·(-1)⁴=10·1=10

б) 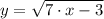$\displaystyle y=\sqrt{7 \cdot x-3}$ , x₀= 1

$\displaystyle y'=(\sqrt{7 \cdot x-3})' =((7 \cdot x-3)^{\frac{1}{2} })'=\dfrac{1}{2} \cdot (7 \cdot x-3)^{\frac{1}{2}-1} \cdot (7 \cdot x-3)'=\\\\=\dfrac{1}{2} \cdot (7 \cdot x-3)^{-\frac{1}{2}} \cdot 7=\dfrac{7}{2} \cdot (7 \cdot x-3)^{-\frac{1}{2}}$

$\displaystyle y'(1)=\dfrac{7}{2} \cdot (7 \cdot 1-3)^{-\frac{1}{2}}=\dfrac{7}{2} \cdot 4^{-\frac{1}{2}}=\dfrac{7}{2} \cdot 2^{-1}= \dfrac{7}{2} \cdot\frac{1}{2}=\dfrac{7}{4}=1\dfrac{3}{4}$

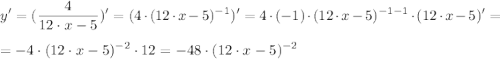
в) $\displaystyle y=\frac{4}{12 \cdot x-5}$ , x₀= 2 $\displaystyle$ $\displaystyle y'=(\frac{4}{12 \cdot x-5})'=(4 \cdot (12 \cdot x-5)^{-1})'=4 \cdot (-1) \cdot (12 \cdot x-5)^{-1-1} \cdot (12 \cdot x-5)'=\\\\=-4 \cdot (12 \cdot x-5)^{-2} \cdot 12=-48 \cdot (12 \cdot x-5)^{-2}$

$\displaystyle y'(2)=-48 \cdot (12 \cdot 2-5)^{-2}= \frac{-48 }{19^{2}}=-\frac{48 }{361}}$

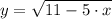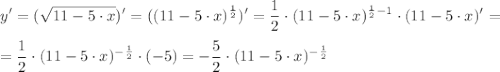
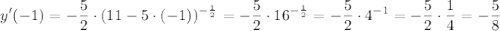
г) $\displaystyle y=\sqrt{11-5 \cdot x}$ , x₀= -1 $\displaystyle y'=(\sqrt{11-5 \cdot x})' =((11-5 \cdot x)^{\frac{1}{2} })'=\dfrac{1}{2} \cdot (11-5 \cdot x)^{\frac{1}{2}-1} \cdot (11-5 \cdot x)'=\\\\=\dfrac{1}{2} \cdot (11-5 \cdot x)^{-\frac{1}{2}} \cdot (-5)=-\dfrac{5}{2} \cdot (11-5 \cdot x)^{-\frac{1}{2}}$ $\displaystyle y'(-1)=-\dfrac{5}{2} \cdot (11-5 \cdot (-1))^{-\frac{1}{2}}=-\dfrac{5}{2} \cdot 16^{-\frac{1}{2}}=-\dfrac{5}{2} \cdot 4^{-1}= -\dfrac{5}{2} \cdot \frac{1}{4}=-\dfrac{5}{8}$

3. Найдите производные функций:

a) y=(x-1)·(x²+x+1) = x³-1

=1·(x²+x+1)+(x-1)·(2·x+1)= x²+x+1+2·x²+x-2·x-1 =3·x²

б) $\displaystyle y=\frac{x^{9}-3}{x^{3}}$

$\displaystyle y'=(\dfrac{x^{9}-3}{x^{3}})'=\dfrac{(x^{9}-3)' \cdot x^{3}-(x^{3})' \cdot (x^{9}-3)}{(x^{3})^{2}}=\\\\=\dfrac{(9 \cdot x^{8}-0) \cdot x^{3}-(3 \cdot x^{2}) \cdot (x^{9}-3)}{x^{6}}=\dfrac{9 \cdot x^{8}\cdot x^{3}-3 \cdot x^{2} \cdot (x^{9}-3)}{x^{6}}=\\\\=\dfrac{9 \cdot x^{11}-3 \cdot x^{11} +9\cdot x^{2}}{x^{6}}=\dfrac{6 \cdot x^{11}+9\cdot x^{2}}{x^{6}}=\dfrac{6 \cdot x^{9}+9}{x^{4}}$

$\displaystyle y'=(\dfrac{x^{9}-3}{x^{3}})'=(x^{6}-\dfrac{3}{x^{3}})'=(x^{6}-3 \cdot x^{-3})'=(x^{6})'-3 \cdot (x^{-3})'=\\\\= 6 \cdot x^{5}-3 \cdot (-3) \cdot x^{-4}=6 \cdot x^{5}+9\cdot x^{-4}=\dfrac{6 \cdot x^{9}+9}{x^{4}}$

4,5(12 оценок)

Ответ:

anvasilovsckay

09.05.2023

В задании где-то ошибка. Дело в том, что заданный график функции y=3x²-6x это парабола, ветви которой направлены вверх, вершина параболы находится в точке с координатами (1;-3), поэтому в точке (1;-4) не может быть точка касания.
Если предположить, что точка касания (1;-3), то решение будет следующим:
Уравнение касательной
y=f(x₀)+f'(x₀)(x-x₀)
Так как (1;-3) точка касания, то x₀=1 f(x₀)=-3
Остаётся найти производную и, затем, её значение в точке х₀=1
f'(x)=(3x²-6x)'=6x-6
f'(1)=6*1-6=0
Подставляем все найденные значения в уравнение касательной
y=-3+0*(x-1)=-3
Уравнение касательной - прямая параллельная оси ОХ, проходящая через точку у=-3.

4,8(96 оценок)

Это интересно:

07.06.2020

Отличный способ провести каникулы - морское путешествие! Как правильно подготовиться к нему?...

Компьютеры-и-электроника

09.11.2021

Как скачать приложения на Android: пошаговая инструкция для начинающих...

Компьютеры-и-электроника

18.09.2022

Как добавить кнопку Facebook на свой сайт: шаг за шагом...

Транспорт

14.01.2023