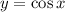
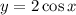
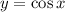 . Отличается лишь область значений.
. Отличается лишь область значений.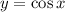 область значений следующая:
область значений следующая:![E(\cos x)=[-1,1]](/tpl/images/0579/2389/1dd9b.png)

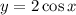 :
: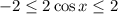
![E(y)=[-2,2]](/tpl/images/0579/2389/4690c.png)
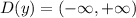 - область определения
- область определения 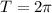 - период функции (все тригонометрические функции периодичны) .
- период функции (все тригонометрические функции периодичны) .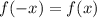
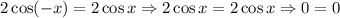 - тождество.
- тождество.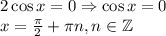
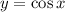 достигает экстремумы на концах отрезка области значения, то и
достигает экстремумы на концах отрезка области значения, то и 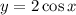 достигает экстремумы на концах отрезка:
достигает экстремумы на концах отрезка:![[-2,2]](/tpl/images/0579/2389/82b6c.png)
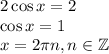 - максимумы.
- максимумы.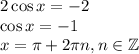 - минимумы.
- минимумы. и на интервалах, получаемые сдвигом этого интервала на
и на интервалах, получаемые сдвигом этого интервала на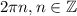
 и на интервалах, получаемые сдвигом этого интервала на
и на интервалах, получаемые сдвигом этого интервала на 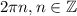
![[\pi,2\pi]](/tpl/images/0579/2389/a222e.png) и на отрезках, получаемых сдвигами этого отрезка на
и на отрезках, получаемых сдвигами этого отрезка на 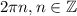
![[0,\pi]](/tpl/images/0579/2389/2a07b.png) и на отрезках, получаемых сдвигами этого отрезка на
и на отрезках, получаемых сдвигами этого отрезка на 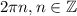

осталось ? км, но на 75 км>, чем проехал.
путь ? км
Решение.
100 % весь путь в %;
100 - 25 = 75 (%) остаток пути в %;
75 - 25 = 50 (%) разница остатка и уже пройденного пути в %;
50% = 75 км по условию;
75 * 100 : 50 = 150 км весь путь в км;
ответ: 150 км длина всего пути;
Проверка: 150*(100-25)% - 150*25% = 75; 75=75