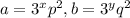, где p и q - натуральные числа, не делящиеся на 3. Ясно, что x<n, y<n. Если x=y, то, разделив обе части на 
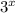, получим уравнение 
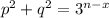. Поскольку числа p и q не делятся на 3, а величина n-x больше 0, это уравнение корней не имеет. Наконец, рассмотрим случай, когда x≠y, в силу симметрии можно считать, что x<y. Разделив уравнение на 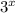, имеем 
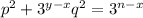. Первое слагаемое не делится на 3, второе и третье делятся, получили противоречие.
2100 дм².
Пошаговое объяснение:
1-й вычитание из площади, рассчитанной по размерам внешнего контура.
1) Площадь, рассчитанная по размерам внешнего контура:
60 * 50 = 3000 дм² .
2) Вычитаемая площадь - это прямоугольник со сторонами:
АК = ВС - МД = 60-30 = 30 дм,
КМ = СД - ВА = 50-20 = 30 дм.
30 * 30 = 900 дм².
3) Площадь заштрихованной фигуры АВСДМК:
3000-900=2100 дм².
2-й суммирование площадей.
АВСДМК состоит из 2-х прямоугольников со сторонами:
1) ВА=20 дм и АК = ВС-МД = 60-30=30 дм; площадь этого прямоугольника равна:
20*30 = 600 дм²;
2) МД = 30 дм и СД = 50 дм; площадь этого прямоугольника равна:
30 * 50 = 1500 дм²;
Таким образом общая площадь АВСДМК равна:
600 + 1500 = 2100 дм².
Мы получили такой же результат.
