1. разделить 90
всего частей
8+2+5 = 15 частей
размер одной части
90 : 15 = 6 - одна часть
находим части числа 90:
6*8=48, 6*2=12, 6*5=30 - части числа - ответ
наибольшая часть: 48 - ответ
2. пропорция про трубы.
24 мин * 6 шт = х мин * 9 шт - работа - обратная пропорциональность
х = 24*6: 9 = 144 : 9 = 16 мин - время наполнения - ответ
3. нет описания фигуры.
4. нет результатов измерений карты.
м 1: 30 000 000 - (неименованный) масштаб - дано
в 1 см - 30 000 000 см = 300 000 м = 300 км
k = 300 км/см - именованный масштаб.
в 1 мм - 30 км. измеряем с точностью до миллиметров и умножаем.
3. периодические дроби
0,(7) = 7/9 0,(1) = 1/9
2,4(3) = 2 13/30
правило перевода дробей на рисунке в приложении.
4. мотоциклист догоняет.
vc = s/tc = 23,4 : 32 = 117/160 = 0,73125 - скорость сближения - погони.
v2 = v1 + vc = 13.5 + 0.73125 = 14.23125 - скорость мотоциклиста - ответ
исправляем - наверно не 32 часа, а 32 минуты
переводим минуты в часы:
tc = 32 мин = 32/60 ч = 8/15 ч - время сближения.
vc =s/tc = 23 2/5 : 8/15 = 43 7/8 км/ч = скорость сближения
vm = 13 1/2 + 43 7/8 = 59 3/8 = 59,375 км/ч - скорость мотоцикла - ответ
ответ: min y = -3, max y = -1.
Пошаговое объяснение:
Находим производную.
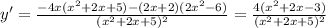
Приравниваем нулю множитель числителя с переменной.
Решаем уравнение x^2+2*x-3=0.
Ищем дискриминант:
D=2^2-4*1*(-3)=4-4*(-3)=4-(-4*3)=4-(-12)=4+12=16;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√16-2)/(2*1)=(4-2)/2=2/2=1;
x_2=(-√16-2)/(2*1)=(-4-2)/2=-6/2=-3.
Находим знаки производной в промежутках между критическими точками.
x = -4 -3 0 1 2
y' = -0,118343 0 0,48 0 -0,118343 .
Как видим, в точке х = -3 минимум функции, а в точке х = 1 - максимум.
Находим значения функции в этих точках.
у(-3) = (-2(9+3))/(9-6+5) = -24/8 = -3.
у(1) = (-2(1+3))/(1+2+5) = -8/8 = -1.
На заданном промежутке [-5; 1] значение функции у(1) = -1 является максимальным, а у(-3) =-3 минимальным.
1) 17,6 * 2 = 35,2 см - сумма оснований
2) (35,2 - 2,6) : 2 = 32,6 : 2 = 16,3 см - малое основание - ОТВЕТ
3) 16,3 + 2,6 = 18,9 см - большое основание - ОТВЕТ