Четное число должно делиться без остатка. Без точек, запятых, и чисел после них. Если вы разделили число на два, и получили дробный результат - знайте число нечетное. Какое перед вами число, четное или нечетное, можно определить по последнему знаку самого числа. Четные числа обычно имеют на конце следующие четные цифры: 0 2 4 6 8. Два числа называются числами одинаковой четности, если оба они четные или оба нечетные. Числа разной четности - это когда одно число четное, а второе нечетное. Сложение и вычитание четных и нечетных чисел: Чётное ± Чётное = Чётное Чётное ± Нечётное = Нечётное Нечётное ± Нечётное = Чётное
) x + a = 7 <=> x = 7 – a, то есть решение к данному уравнению найдено. Для различных значений параметров, решения есть x = 7 – a
B) 2x + 8a = 4 <=> 2x = 4 - 8a <=> x = 2 – 4a
C) x + a = 2a – x <=> x + x = 2a – a <=> 2x = a <=> x = a/2
D) ax = 5, когда а отличается от 0 мы можем разделить обе части на a и мы получим x = 5 Если a = 0, мы получим уравнение, такое как 0.x = 5, и которое не имеет решения;
E) a – x = x + b <=> a – b = x + x <=> 2x = a – b <=> x = (a – b)/2
F) Когда a = 0 уравнение ax = 3a равно 0.x = 0 Поэтому, любое x является решением. Если a отличается от 0, тогда ax = 3a <=> x = 3a/a <=> x =
Чтобы решать, нужно привести уравнения к одному виду:
2х-у=6 х+2у=8
у= -2х+6 у=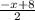
Чтобы найти точку пересечения прямых, нужно приравнять оба уравнения:
-2х+6 =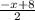
Чтобы решить пользуемся свойством пропорции:
2(-2х+6) = 1(8-х)
-4х+12 = 8-х
-3х = -4
х = 1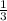 - это ордината точки
- это ордината точки
Теперь найдем абциссу, подставив в первоначально уравнение х:
2у = 8-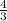
2у =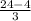
у =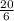
у =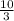
у = 3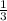
Итак, мы получили точку: (1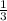 ;3
;3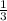 )
)
Удачи от Беллы