1. Тема памяти. В рассказае Борис Васильев обличает бесчеловечную разлагающую силу формализма. Для Анны Федотовны письма - это память о сыне, целая жизнь, а для юных пионеров всего лишь забытый экспонат.
2. Образ игоря в рассказе создается от взрослого мужчины ушедшего на фронт к маленькому мальчику, безотцовщине каким его знала только мать Анна Федоровна - бес ползающим, топающим, убегающим в Испанию или решающим непонятные ей задачи, - в конце концов он непременно вставал перед ней медленно спускающимся с первого лестничного марша. И каждый вечер она видела его узкую спину и слышала одну и ту же фразу: - Я вернусь, мама.
Характер Игоря: Игорь рос тихоней, с удовольствием подчинялся своему другу Володьке. (Игорек бежал в Испанию. Мальчики, обреченные на безотцовщину растут либо отчаянными неслухами, либо тихонями, и ее сын склонялся к последнему типу).Из письма его друга мы видим, что Игорь всегда являлся примером для всего отряда.("Ваш Игорь, дорогая Анна Федотовна, всегда являлся примером для всего нашего отделения..."
2х+3у-7=0
Пошаговое объяснение:
1) Нужно найти координаты вершины А. Очевидно, что она лежит на пересечении прямых АВ и АС, т.е. у этой точки значения у и х будут принадлежать области значений и определения обеих функций. Другими словами, нам нужно решить систему их уравнений.
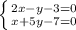
Из уравнения АВ: у=2х-3,
подставляем в уравнение АС: х+5·(2х-3)-7=0
х+10х-15-7=0
11х=22
х=2
у=2·2-3=1
Итого, имеем координаты вершины А(2;1).
2) Нужно составить общее уравнение прямой а, проходящей через точку А и перпендикулярную прямой ВС.
Так как прямая а перпендикулярна прямой ВС, то направляющий вектор прямой а есть нормальный вектор заданной прямой 3x-2y+13=0, то есть, направляющий вектор прямой а имеет координаты (3;-2).
Теперь мы можем записать каноническое уравнение прямой а на плоскости, так как знаем координаты точки А, через которую проходит прямая а, и координаты направляющего вектора прямой а:
=
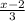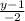. (Здесь в числителях задействованы координаты точки А, в знаменателях - координаты напрявляющего вектора)
От полученного канонического уравнения прямой a перейдем к общему уравнению прямой:
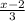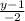= ⇒ -2·(х-2)=3·(у-1) ⇒ 2х+3у-7=0.
ответ: уравнение высоты, проведенной через вершину A 2х+3у-7=0
