Дано:
S = 203 км - расстояние АВ.
m = 100 км/ч - скорость второго
t1 = 3 ч - время задержки второго
Найти: Sc = ? - расстояние АС.
Пошаговое объяснение:
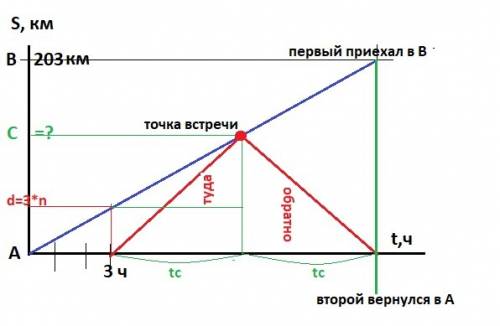
Делаем схему движения - рисунок в приложении. n - скорость первого.
Постановка задачи: АС = m*tc = 110*tc. Найти - tc- время "погони".
Можно написать такие уравнения:
1) d = n*t1 = 3*n - дистанция "погони" - первый "убежал".
2) tc = d/(m-n) - время до встречи "погони"
3) T = S/n = 203/n - время в пути первого - прибыл в пункт В.
4) Т = 3 + 2*m*tc - одновременно - первый прибыл в пункт В, а второй вернулся в пункт А.
Пробуем составить окончательное уравнение.
5) 203/n = 3 + 2*3*n/(110-n)
203/n = 3 + 6*n/(110-n)
6) 203*(110-n) = 3*n*(110-n) + 6n²
7) 22330 - 203*n = 330*n - 3n² + 6n²
8) 3*n² - 127*n - 22330 = 0
Решаем квадратное уравнение и получаем:
D = 284089, √D = 533, и два корня: n1 = 110 и УРА - n = 67 2/3 (≈67.(6))
Дальше не решается, где-то ошибки, но может быть подсказка
29 т 20 кг - с I участка
? т - со II участка, на 4 т 960 кг >, чем с I
? т - увезли с каждого, на ? т <
1 т = 1 000 кг
1) 29 т 20 кг + 4 т 960 кг = (29 * 1 000 + 20) + (4 * 1 000 + 960) = 29 020 + 4 960 = 33 980 кг = 33 т 980 кг - собрали со II участка
2) 29 т 20 кг - 6 т 30 кг = 29 020 - (6 * 1 000 + 30) = 29 020 - 6 030 = 22 990 кг = 22 т 990 кг - увезли с I участка
3) 33 т 980 кг - 5 т 60 кг = 33 980 - (5 * 1 000 + 60) = 33 980 - 5 060 = 28 920 кг = 28 т 920 кг - увезли со II участка
3) 28 920 - 22 990 = 5 930 кг = 5 т 930 кг - на столько меньше с I участка
ответ: с первого участка увезли на 5 т 930 кг свеклы меньше, чем со второго.
Ну короче, я так думаю:
Путь мы можем любой положить, я возьму S=2 м:
t=S/(x+y); 40=2/(x+y);
xT₁=S; 72x=2;
x=1/36;
x+y=1/20;
1/36+y=1/20;
y=1/45 м/с;
T₂=2/(1/45)=90 минут;
ответ: 90 минут.