Итак, для ограничения по целым степеням не более 27 по модулю, вычислимыми оказались результаты ~957 млн выводов и среди них 356 являются выводами числа 5479 и ни один вывод (а соответственно ни один вывод с операциями сложения, вычитания, конкатенации, умножения и деления, а также некоторые выводы с этими же операциями и некоторыми целыми степенями) не является выводом числа 10958. В чем его особенность?
Призраки и тени
Для задачи, аналогичной задаче Танежи в восходящем порядке, но с начальными векторами длины 8, такими как $(1, 2, ... , 8)$ и $(2, 3, ... , 9)$ количество вариантов меньше, а с иррациональными, комплексными и длинными целыми значениями элементов векторов (1) — (7) справляются оптимизированные алгоритмы Вольфрам Математики. Так, достоверно известно, что ни один вывод в $(1, 2, ... , 9)$, имеющий на 8-ой итерации оператор конкатенации, сложения или вычитания не может привести к значению 10958. Какие возможности для дальнейшего решения это даёт?
Число 10958 является полупростым. И если последняя итерация вывода не содержит сложение, вычитание и конкатенацию, то один из операндов на 8-ой итерации будет гарантировано включать 5479 в некоторой степени, за исключением двух случаев:
когда операнды кратны некоторым комплексно-сопряжённым
когда один из операндов содержит логарифм, основание или показатель которого кратны 5479
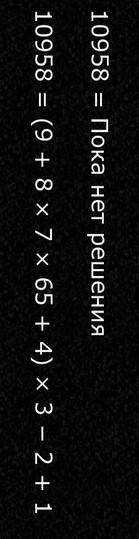
14,5
Пошаговое объяснение:
S1 = 35 км
t1 = 3 год
t = 7 год
U1 = 3 км/час
t2 - ?
U - ?
U2 - ?
Розв'язання:
Загальна подорож тривала 7 годин, віднімемо 3 години на зупинці, отримаємо 2 години.
1) t2 =t - t1 = 7 - 3 = 4 години - плили туди і в зворотньому напрямку
2) U = U1 * t2 = 3*4 = 12 км/час - заняла швидкість течії річки за 4 години
3) S = S1 * 2 = 35 * 2 = 70 км - загальна пройдена відстань
4) U2 =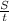 
= 
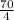= 17,5 км/год - швидкість катера з течією.
5) U = U2 - U1 = 17,5 - 3 = 14,5 км/год - швидкість катера без течії у стоячій воді
