400
Пошаговое объяснение:
Требуется вычислить сумму
S = 1 + 3 + 5 + ... + 35 + 37 + 39
Количество слагаемых равно (39-1):2+1=38:2+1=19+1=20.
Первый член арифметической прогрессии a₁=1, разность d=2. Нужно вычислить сумму первых n=20 членов прогрессии. Так как последний член прогрессии a₂₀=39, то можно использовать формулу
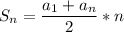 .
.
Тогда
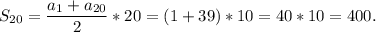
Перепишем сумму в двух видах
S = 1 + 3 + 5 + ... + 35 + 37 + 39
S = 39 + 37 + 35 + ... + 5 + 3 + 1
Так как количество слагаемых 20, то сумма обоих сумм равна
2·S = (1+39)+(3+37)+(5+35)+ ... +(5+35)+(3+37)+(1+39) =
=40+40+40+...+40+40+40=40·20
или
S = 40·20:2= 800:2=400.
тогда в см сторона другого квадрата.
а-2 см, в-2 см уменьшили стороны каждого квадрата на два,
(а-2)²-(в-2)²=28
5/4=а/в
а=5/4в
(а-2)²-(в-2)²=28
а²-4а+4-(в²-4в+4)=28
а²-4а+4-в²+4в-4=28
а²-в²-4а+4в-28=0
(5/4в)²-в²-4*5/4в+4в-28=0
25/16в²-в²-5в+4в-28=0
1 9/16в²-в²-в-28=0
9/16в²-в-28=0
D=1-4*9/16*(-28)=1+9/4*28=1+9*7= 1+63=64 (8²)
в1=1+8 / 2*9/16= 9 / 9/8= 9*8/9=8
в2=1-8 / 2*9/16= -7 / 9/8= -7 * 8/9= -56/9= - 6 2/9 < 0, не удовлетворяет условию задачи
а=5/4*8=5*2=10
ответ: 8см и 10см