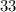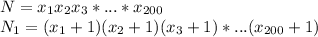
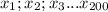Сооружения из камня, являющееся знаком вечности, символом мощи, богатства, значимости фараона

👇

Увидеть ответ

Ответ:

Pyc52141

05.02.2022

Египетские пирамиды.

4,5(85 оценок)

Ответ:

klimkravcnko

05.02.2022

Египетские пирамиды,

4,7(49 оценок)

Открыть все ответы

Ответ:

хххх555555пауотаг

05.02.2022

Запишем условие $N=x_{1}x_{2}x_{3}*...*x_{200}\\ N_{1}=(x_{1}+1)(x_{2}+1)(x_{3}+1)*...(x_{200}+1)\\$
где $x_{1};x_{2};x_{3}...x_{200}$ - простые числа
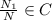По условия $\frac{N_{1}}{N} \in C$ целое .
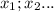Если все числа $x_{1};x_{2}...$ будут действительно различные, то из выражения
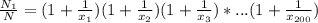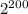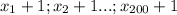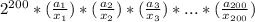$\frac{N_{1}}{N}= (1+\frac{1}{x_{1}})(1+\frac{1}{x_{2}})(1+\frac{1}{x_{3}})*...(1+\frac{1}{x_{200}})$ с учетом того что данные числа простые, как минимум среди них будет множитель $2^{200}$ ,потому что $x_{1}+1;x_{2}+1...;x_{200}+1$ уже четные числа. Запишем как $2^{200}*(\frac{a_{1}}{x_{1}})*(\frac{a_{2}}{x_{2}})*(\frac{a_{3}}{x_{3}})*...* (\frac{a_{200}}{x_{200}})$ так как $a_{n}$
То следует что, числа в каждой дроби будут взаимно простые между собой.
То есть не дадут целое числа в итоге, теперь рассмотрим случаи когда числа равные между собой, то есть предположим что среди них есть числа равные между собой .
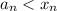
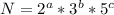
для начало положим что N=2^a*3^b*5^c

откуда получаем , после преобразований
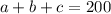
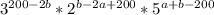
$3^{200-2b}*2^{b-2a+200}*5^{a+b-200}$
так как числа все простые , то есть не одно число не делится на другой без остатка , то
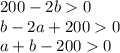
$200-2b0\\
b-2a+2000\\
a+b-2000$
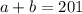откуда с последнего неравенства, решения будут при целых a+b=201

то есть все числа должны давать в сумме 201

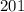, но тогда

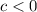что не противоречит условию
Теперь увеличим наше число до

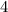простых числа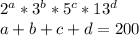
$2^a*3^b*5^c*13^d\\
a+b+c+d=200\\

$
так же после всех преобразований получаем
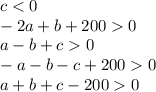
$c0\\a-b+c0\\-a-b-c+2000\\a+b+c-2000$
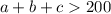но отсюда так же следует что a+b+c200

что противоречит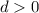

И теперь очевидно для

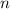взятого простого числа так же будет справедлива это тождество.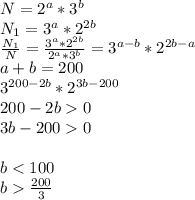

Теперь рассмотрим случай $N=2^a*3^b\\
N_{1}=3^a*2^{2b}\\
\frac{N_{1}}{N} = \frac{3^a*2^{2b}}{2^a*3^b} = 3^{a-b}*2^{2b-a}\\
a+b=200\\
3^{200-2b}*2^{3b-200}\\
200-2b0\\
3b-2000\\\\
b\frac{200}{3}$
откуда $[ \frac{200}{3} ]= 66\\
100-66=33$ решения
ответ

И это все является решением для 6-классника, так как использованы обычные работы со степенями и неравенствами

4,8(70 оценок)

Ответ:

kavilochka

05.02.2022

Амур - дождевой и летнее половодье, Анадырь - подземные воды, Волга - дождевые и талые воды (снеговое) , Днепр - дождевые и талые воды (больше преобладают талые воды) , Дон - талые воды (снеговое) , Енисей - дождевые и талые воды (снеговое) , Индигирка - не знаю, Колыма - дождевые и подземные грунтовые воды, Лена - дождевые и талые воды (больше преобладают талые воды) , Нева - подземные грунтовые воды, Обь - дождевые и талые воды (снеговое) , Печора - талые воды (снеговое) , Северная Двина - талые воды (снеговое) , Урал - талые воды (снеговое) , Яна - дождевой.

4,8(86 оценок)

Это интересно:

Компьютеры-и-электроника

10.03.2023

Как сделать снимок в Windows Live Movie Maker: подробное руководство...

Компьютеры-и-электроника

28.05.2023

Как создать ISO файл в Linux: шаг за шагом руководство...

08.02.2021

Как найти счастье и любить себя, когда жизнь кажется трудной и неподатливой?...

Образование-и-коммуникации

11.07.2021