а) 102 б) 105
Пошаговое объяснение:
Задание
Найти наименьшее трёхзначное число, которое делится:
а) на 6 (т.е на 3 и на 2)
б) на 15 (т.е на 3 и на 5)
Решение
Наименьшее трёхзначное число - это число, которое равно или больше 100.
а)
Наименьшее трёхзначное число, которое делится на 6, должно удовлетворять двум признакам делимости:
1) быть чётным (признак делимости на 2);
2) сумма его цифр должна делиться на 3 (признак делимости на 3).
Наименьшее трёхзначное число 100 является чётным (делится на 2), но 3 не делится (даёт в остатке 1). Следовательно, к 100 необходимо прибавить 2 - в этом случае полученное число будет чётным, а его сумма цифр (1+0+2=3) будет делиться на 3:
100 + 2 = 102.
Таким образом, полученное число 102 делится на 2 и на 3, а значит, делится и на 6.
Проверка: 102 : 6 = 17
ответ: 102.
б)
Наименьшее трёхзначное число, которое делится на 15, должно удовлетворять двум признакам делимости:
1) заканчиваться цифрой 0 или 5 (признак делимости на 5);
2) сумма его цифр должна делиться на 3 (признак делимости на 3).
Наименьшее трёхзначное число 100 заканчивается нулём (делится на 5), но при делении на 3 даёт в остатке 1.
Следовательно, к 100 необходимо прибавить 5 - в этом случае полученное число будет заканчиваться цифрой 5, а сумма его цифр (1+0+5=6) будет делиться на 3:
100 + 5 = 105.
Таким образом, полученное число 105 делится на 3 и на 5, а значит, делится и на 15.
Проверка: 105 : 15 = 7
ответ: 105.
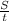

2)4 1/4-2 2/4=1 3/4
3)20:7 13/14=20/1:111/14=280/111=2 58/111
4)1 3/4:5=7/4:5/1=7/20
5)2 58/111-7/20=2 383/2220