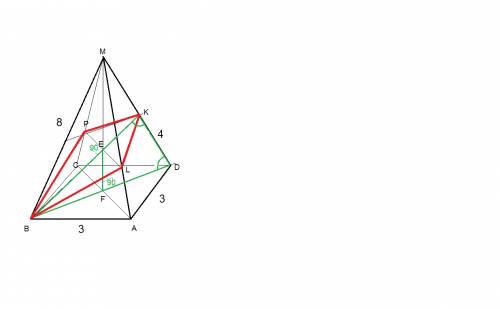
искомое сечение - симметричный четырехугольник BPKL
диагонали PL , BK пересекаются под углом 90 град
по условию
стороны основания AB=BC=CD=AD =3
боковые ребра MA=MB=MC=MD =8
точка К - середина ребра MD ; KD = MD /2 = 8/2=4
ABCD -квадрат
диагональ AC = BD = 3√2
пересечение диагоналей точка F : BF =FD = BD/2 =3√2 /2 =1.5√2
BK - медиана треугольника MBD
длина медианы BK = 1/2 √(2 BM^2 +2 BD^2 - MD^2 ) =1/2 √(2*8^2 +2*(3√2)^2 - 8^2 ) =5
по теореме косинусов
cos KBD = ( KD^2 - (BK^2+BD^2) )/ (-2*BK*BD)= ( 4^2 - (5^2+(3√2)^2) )/ (-2*5*3√2)= 9/(10√2)
MF - высота
треугольник EBF - прямоугольный
BE = BF / cos KBD = 1.5√2 / [ 9/(10√2)] = 10/3
по теореме Пифагора EF =√(BE^2 - BF^2) =√( (10/3)^2 - (1.5√2)^2) =√238/6
MF - высота
треугольник MFB - прямоугольный
по теореме Пифагора MF =√( MB^2 -BF^2) =√( 8^2- (1.5√2)^2 ) =√238/2
ME =MF -EF =√238/2- √238/6= √238/3
треугольники MPL ~ MCA подобные
PL / AC = ME /MF ; PL = AC * ME /MF = 3√2 * √238/3 /√238/2 =2√2
площадь сечения(четырехугольника BPKL)
Sс = PL*BK *sin<BEP /2 = 2√2*5*sin90 /2 = 5√2
ответ 5√2
а) 2,2,4
б) нет. Наименьшее из написанных чисел - наименьшее из загаданных чисел; наибольшее - сумма загаданных чисел. Так, среди загаданных чисел есть 1, а сумма всех чисел равна 22. Но сумма всех чисел без единицы 22-1=21 не выписана.
в) Сумма чисел 52. Наименьшее число равно 9. 10, 11 - также загаданные числа (это не может быть суммой 9 и какого-то числа, не меньшего 9).
19 = 10 + 9; 43 = 52 - 9
20 = 11 + 9; 42 = 52 - 10
21 = 10 + 11; 41 = 52 - 11
22 = ? 33 = 52 - 10 - 9
30 = 52 - 22; 32 = 52 - 11 - 9
31 = 52 - 10 - 11
Рассмотрим случаи.
а) Число 22 среди загаданных. Тогда 30=52-22, загаданные числа 9, 10, 11, 22 - их сумма 52, и все "частичные суммы" выписаны.
б) Число 22 не среди загаданных. Тогда 22 - какая-то сумма составленная из чисел 9, 10, 11 (взятыми произвольное (возможно, нулевое) число раз).
9 не может входить в эту сумму (22-9=13 невозможно получить сложением этих чисел).
Аналогично, 10 не входит в эту сумму. Итак, 22 = 11 + 11 и 11 взято как минимум 2 раза.
Уже известные числа: 9, 10, 11, 11 - сумма 41. Оставшееся число равно 52-41=11. Легко проверить, что этот набор чисел также удовлетворяет условию.
ответ.
а) 2,2,4
б) нет
в) {9, 10, 11, 22} или {9, 10, 11, 11, 11}