Пошаговое объяснение:
1)
уравнение прямой, проходящей через точку
y = y(х₀) + y'(x₀)(x - x₀)
По условию задачи x₀ = -2,
найдем тогда y(х₀) = 16
Теперь найдем производную:
y' = (3*x2-2*x)' = 6x-2
у'(-2) = 6*(-2)-2 = -14
теперь все подставим в уравнение касательной и получим
y=16+(-14)(x--2) ;
y = -14x-12
теперь нормаль
общий вид нормали
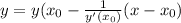
все данные у нас есть, поэтому запишем сразу уравнение нормали
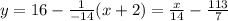
2) y₁=2x², y₂=0, x₁=-1, x₂=2
площадь фигура равна
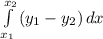
поскольку у нас все есть, просто считаем определенный интеграл
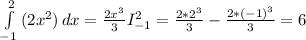
Пошаговое объяснение:
f'(t) = 3t^2 - 18t + 2 = 0
D4 = 81 - 6 = 75 = (5√3)^2
t1,2 = (9 ± 5√3)/3 = 3 ± 5/3 * √3
+ - +
3 - 5/3 * √33 + 5/3 * √3
/ \ /
Возрастает: x ∈ (-∞; 3 - 5/3 * √3] U [ 3 + 5/3 * √3; +∞)
Убывает: x ∈ [3 - 5/3 * √3; 3 + 5/3 * √3]
У Вас тут t с х смешалось, поэтому я подразумеваю, что t0 = 3
Уравнение касательной: f(t) = f'(t0) * (t - t0) + f(t0)
f'(t0) = 3*3^2 - 18*3 + 2 = -25
f(t0) = 3^3 - 9*3^2 + 2*3 +30 = -18
f(t) = -25 * (t - 3) - 18 = -25t + 57 - уравнение касательной
Графики приложены в вордовском файле