Поскольку x = 0 не является решением данного дифференциального уравнения, то поделим обе части уравнения на , получаем
В левой части уравнения это ни что иное как формула производной частного, то есть :
Подсчитаем отдельный интеграл по частям.
2)
Это линейное однородное дифференциальное с постоянными коэффициентами. Замена , перейдём к характеристическому уравнению: , корни которого и . Тогда общее решение диф. уравнения: и его первая производная .
Осталось найти константы C₁ и C₂ , подставляя начальные условия.
ДАНО S=60 км - расстояние АВ V1-V2=4 - разность скоростей T2=T1+ 01:15 = 1 1/4 ч- время опоздания второго НАЙТИ t2(12)=? - время 2-го на путь в 12 км РЕШЕНИЕ Мысли: 1- опоздал из-за разности скоростей. 2 - используем формулу пути 3- два неизвестных -нужно два уравнения. РЕШЕНИЕ. Уравнение пути S = V*T T=S/V 1) S/V2 - S/V1 = 1 1/4 - разность времен - время опоздания 2) V2 = 4 - V1 Упрощаем уравнение 1) - приводим к общему знаменателю. 3) S/V2-S/V1 =5/4 S*(V1-V2) = 5/4*V1*V2 =5/4V1² - 5*V1 или после умножения на 4. получаем квадратное уравнение. 5V1² -20*V1-960 = 0 Корень уравнения V1 = 16 км/ч ( и V= -12) - скорость 1-го Скорость 2-го V2 = 16-4 = 12 км/ч И время на 12 км пути со скоростью 12 км/ч. t2(12) = 12/12 = 1 час. ОТВЕТ: 2-му велосипедисту потребуется 1 час.
1)
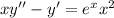
Поскольку x = 0 не является решением данного дифференциального уравнения, то поделим обе части уравнения на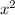
, получаем
В левой части уравнения это ни что иное как формула производной частного, то есть :
Подсчитаем отдельный интеграл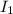
по частям.
2)
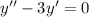
Это линейное однородное дифференциальное с постоянными коэффициентами. Замена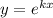
, перейдём к характеристическому уравнению: 
, 
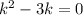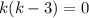корни которого 
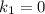и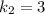 
. Тогда общее решение диф. уравнения: 
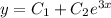и его первая производная 
.
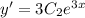Осталось найти константы C₁ и C₂ , подставляя начальные условия.