Question

Алина написала на бумажке числа 5 и a; боря-a, b и 7; сеня написал 3, 9 и c, даня- a, b и 3, а егор написал четыре числа a, b, c, d. всё, что написала алина, написал и даня, а всё, что написано у бори, сени и дани, можно найти и у егора. найдите, чему равны числа a, b, c и d.

Answer 1

Обозначим: Алина - А, Боря - Б, Сеня - С, Даня - Д, Егор - Е.
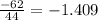
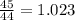
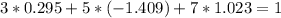
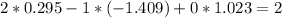
1) Известно:
А: {5, a}
Б: {a, b, 7}
С: {3, 9, c}
Д: {a, b, 3}
Е: {a, b, c, d}
2) Всё, что написала Алина, написал и Даня. То есть 2 числа из 3х, которые есть у Дани, это 5 и a. a явно содержится и там, и там. 7 содержится только у Дани. Делаем вывод, что b=5.
Итого:
А: {5, a}
Б: {a, 5, 7}
С: {3, 9, c}
Д: {a, 5, 3}
Е: {a, 5, c, d}
3) Всё, что написано у Бори, Сени и Дани, можно найти и у Егора.
а) Рассмотрим Б и Е.
Б: {a, 5, 7}
Е: {a, 5, c, d}
Явно видно, что a и 5 содержатся и там, и там. Так как 7 должна содержаться в Е, то 7=c или 7=d
б) Рассмотрим С и Е.
С: {3, 9, c}
Е: {a, 5, c, d}
c содержится в явном виде и там, и там. 3 не может быть 5, 9 не может быть 5. Делаем вывод, что a=3, d=9 или a=9, d=3.
в) Рассмотрим Д и Е.
Д: {a, 5, 3}
Е: {a, 5, c, d}
a и 5 содержатся в явном виде и там, и там. Делаем вывод, что c=3 или d=3.
Нужно распределить числа 3, 7 и 9 между a, c, d. Так как a=3, d=9 или a=9, d=3 (из пункта б), из этого следует, что c=7.
Из пункта в следует, что d=3, т.к. c уже занято 7.
Осталось a=9.
Таким образом, a=9, b=5, c=7, d=3.