Неравенство ax² + bx + c < 0 не будет иметь решений, если парабола
y = ax² + bx + c будет расположена над осью Ох или будет касаться оси.
Для этого коэффициент а должен быть положительным, а уравнение ax² + bx + c = 0 не должно иметь корней или иметь один корень, т.е. дискриминант должен быть меньше либо равен нулю:
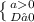
(p - 1) x² + (p - 2) x + 3p - 1 < 0
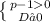
D = (p - 2)² - 4(p - 1)(3p - 1) = p² - 4p + 4 - 12p² + 16p - 4 = - 11p² + 12p
- 11p² + 12p ≤ 0
p(11p - 12) ≥ 0 (см. рис. 1)
p ∈ (- ∞ ; 0] ∪ [12/11 ; + ∞)
p > 1
(см. рис. 2)
p ∈[12/11 ; + ∞)
4,375 - перша машина
5,625 - друга машина
2,5 - третя машина
Пошаговое объяснение:
100%-(35%+45%)=100%-80%=20% - третя машина
45%-20%=25%, тобто на третій на 2,5 менше ніж на другій машині
Нехай 0,35x - перша машина, 0,45x - друга машина, 2,5-x - третя машина
0,35x+0,45x+(2,5-x)=0
0,8x+2,5-x=0
-0,2x+2,5=0
-0,2x=-2,5
0,2x=2,5
x=2,5/0,2=12,5 - 100%
1)12,5*35%=12,5*0,35=4,375 - перша машина
2)12,5*45%=12,5*0,45=5,625 - друга машина
3)12,5*20%=12,5*0,2=2,5 - третя машина
Відповідь:
4,375 - перша машина
5,625 - друга машина
2,5 - третя машина
АЛЕ Я НЕВПЕВНЕНА ЧИ ЦЕ ПРАВИЛЬНО РОЗВ'ЯЗАНА ЗАДАЧА, ПРОТЕ, МОЖЛИВО ЦЕ ОДИН З РОЗВ'ЯЗКІВ