1. Періодичні функції
При введенні тригонометричних функцій аргумент позначався буквою t, оскільки букви х і у використовувались для позначення координат точки Pt . Те-
пер повернемось до звичних позначень: х — незалежна змінна, у — залежна змінна, тобто у = sin х, у = cos х, y = tg x.
Оскільки числам х, х ± 2π на тригонометричному колі відповідає одна й та сама точка Px , то мають місце рівності:
sin(x ± 2π) = sin x, cos(x ± 2π) = cos x .
Цю властивість функцій у = sin х і у = cos х називають періодичністю. Вона полягає у тому, що значення функції повторюються через рівні проміжки зміни аргументу. Точний зміст поняття періодичності функції міститься у наступному означенні.
Функція у = f(х) називається періодичною, якщо існує таке число T ≠ 0, що область визначення функції
разом з кожною точкою х містить точки х ± Т і при цьому виконується рівність f(х ± Т) = f(x). Число Т називається періодом функції.
1) x²−7x−8 < 0
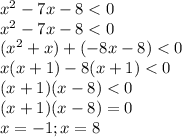
Определяем знаки на промежутках:
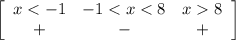
Интервал −1 < x < 8 — удовлетворяет неравенство
Точки выколотые, так как неравенство строгое, — их в ответ не вносим.
ответ: x ∈ (−1; 8).
2) 3x²−4x+7 ≥ 0
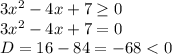
корней нет
делим обе части неравенства на 3х²−4х+7, 3х²−4х+7>0:
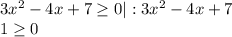
Неравенство выполняется, значит х ∈ R.
ответ: x ∈ (−∞; ∞).
3) x²−2x−3 > 0
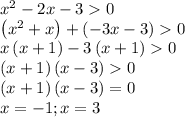
Определяем знаки на промежутках:
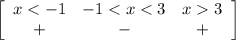
Интервалы x < −1 и x> 3 — удовлетворяют неравенство
Точки выколотые, так как неравенство строгое, — их в ответ не вносим.
ответ: x ∈ (−∞; −1) ∪ (3; +∞).