Сначала запишем формулы, которые понадобятся:
Площадь квадрата равна квадрату его стороны:
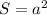
Отсюда, сторона квадрата равна корню квадратному из площади:
Периметр квадрата равен четырём его сторонам:
Подставим в эту формулу вместо стороны a корень из площади, и мы получим вот что:
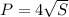
Так считается периметр для квадрата с площадью S
А если взять площадь в девять раз больше (то есть 9S ), то получим периметр P₂ , который равен:
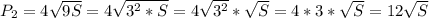
Во сколько раз увеличился периметр? Поделим новый периметр на старый, и узнаем (хоть это и так тут уже понятно).
Периметр увеличился в:
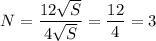(раза)
ответ: периметр увеличится в 3 раза
См. Пошаговое объяснение
Пошаговое объяснение:
Для решения обеих задач используются следующие свойства углов:
1) вертикальные углы равны.
2) развёрнутый угол равен 180°.
а)
∠СОЕ = ∠FOD - как углы вертикальные; следовательно:
2х - 30° = х + 10°
х = 40°
∠СОЕ = 2х - 30 = 2 · 40 - 30 = 80 - 30 = 50°
∠FOD = ∠СОЕ = х + 10 = 40 + 10 = 50°
∠СОF = ∠EOD = 180° - 50° = 130°
∠FOD = ∠СОЕ = 50°
∠СОF = ∠EOD = 130°
b)
∠СОЕ = ∠FOD - как углы вертикальные; следовательно:
4х - 35 = 2х + 21
2х = 56
х = 28°
∠СОЕ = 4х - 35 = 4 · 28 - 35 = 112 - 35 = 77°
∠FOD = ∠СОЕ = 2х + 21 = 2 · 28 + 21 = 56 + 21 = 77°
∠СОF = ∠EOD = 180° - 77° = 103°
∠FOD = ∠СОЕ = 77°
∠СОF = ∠EOD = 103°
