Построить график функции у=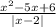 . Найти область определения функции
. Найти область определения функции
Пошаговое объяснение:
у=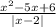 . Разложим х²-5х+6 на множители. х²-5х+6=0 ,х=2,х=3
. Разложим х²-5х+6 на множители. х²-5х+6=0 ,х=2,х=3
у=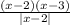
1 случай) Пусть х-2>0, х>2 , тогда |x-2|=x-2
у=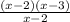 . Область определения функции х≠2 ( при х=2 знаменатель обращается в 0)
. Область определения функции х≠2 ( при х=2 знаменатель обращается в 0)
у=х-3 , х≠2. Графиком является прямая
х -2 3
у -5 0
2 случай) Пусть х-2≤0, х≤2 , тогда |x-2|= -(x-2)
у=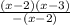 . Область определения функции х≠2 ( при х=2 знаменатель обращается в 0)
. Область определения функции х≠2 ( при х=2 знаменатель обращается в 0)
у=-(х-3) , у=3-х , х≠2. Графиком является прямая
х -2 3
у 5 0
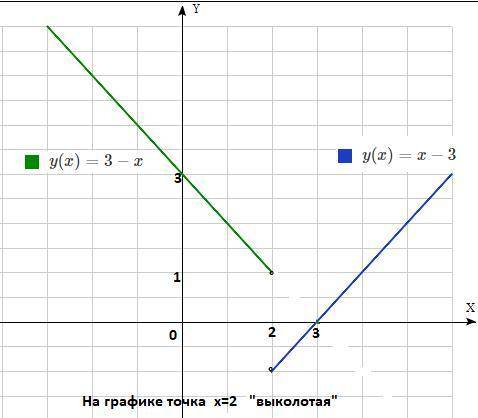
На графике точка х=2 "выколотая"
Область значений функции (-1 ; 1)∪( 1 ;+∞)
ответ: Любая форма клумбы
Пошаговое объяснение:
а) Р=2(a+b)
2(6+8)=28 м
б) Р=2((a-2)+(b-2))
2((6-2)+(8-2))=
2*10=20 м
в) Участок разделен на квадрат 5м х 5 м и 2 прямоугольных треугольника.
Катеты треугольников 2м и 5 м, неизвестная сторона участка - гипотенуза. Формула нахождения длины гипотенузы прямоугоьного треугольника: c²=a²+b². a=2; b=5
c²=2²+5²
c=√29≈5.4 м
Р (участка)=2(a+b), a=5+2=7м, b≈5.4 м
2(7+5.4)=24.8 м
ответ: Обозначение формы осуществляется по периметру выбранного участка.
Самый большой участок имеет периметр 28 м, самый маленький - 20 м, значит 35-и метров ленты хватит, с остатком, на любую форму клумбы.