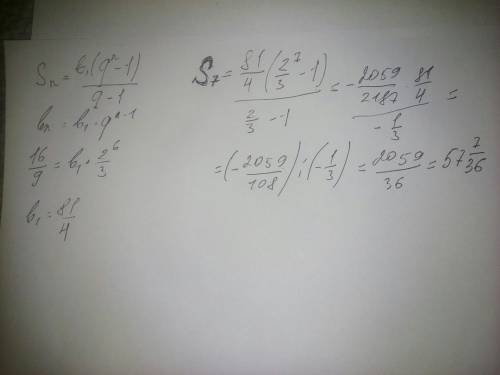
размах ряда чисел - это разность между наибольшим и наименьшим из этих чисел.
среднее арифметическое ряда чисел - это отношение суммы этих чисел на число слагаемых.
мода ряда чисел - это число, которое встречается в этом ряду чаще других.
медиана ряда чисел - это число, стоящее посередине по возрастанию ряда чисел (в случае, если количество чисел нечетное).
медиана ряда чисел - это полусумма двух стоящих посередине чисел по возрастанию ряда (в случае, если количество чисел четное).
1.
размах: 47-25=22;
среднее арифметическое: \frac{39+33+45+25+33+40+47+38+34+33+40+44+45+32+27}{15}= \frac{555}{15}=37
15
39+33+45+25+33+40+47+38+34+33+40+44+45+32+27
=
15
555
=37 ;
мода: 33;
медиана: 38.
2.
размах: 44-30=14;
среднее арифметическое: \frac{36+30+35+36+36+38+40+41+44+43+36+41}{12}= \frac{456}{12}=38
12
36+30+35+36+36+38+40+41+44+43+36+41
=
12
456
=38 ;
мода: 36;
медиана: \frac{38+40}{2}=39
2
38+40
=39 .
3.
размах: 46-24=22;
среднее арифметическое: \frac{34+24+39+36+34+39+38+46+38+34+46+41+43+40}{14}= \frac{532}{14}=38
14
34+24+39+36+34+39+38+46+38+34+46+41+43+40
=
14
532
=38 ;
мода: 34;
медиана: \frac{38+46}{2}=42
2
38+46
=42 .
4.
размах: 58-24=34;
среднее арифметическое: \frac{39+45+35+24+35+38+58+34+38+35+40+42+45+36+56}{15}= \frac{600}{15}=40
15
39+45+35+24+35+38+58+34+38+35+40+42+45+36+56
=
15
600
=40 ;
мода: 35;
медиана: 34.
поскольку 4a<9, то a, которое удовлетворяет этому неравенству это 2(4*2 = 8<9). Ну и по смыслу второго неравенства вижу, что если a по-прежнему равно 2, то получается верное неравенство(3*2>4). Других вариантов у нас нет, так как данное число должно удовлетворять одновременно двум неравенствам. Значит, это число
2.
Либо же можно решить систему неравенств:
4a<9 a<2.25
3a>4 a>1+1/3
Находим разумеется пересечение решений этих неравенств, получаю промежуток:
(1+1/3;2.25). Но нас спрашивали в задаче про целые числа, значит a = 2 из этого промежутка 2 единственное целое число
b1 = 16/9 / (2/3)^6=16/9 * (3/2)^6=(2^4*3^6)/(3^2*2^6)=3^4/2^2=81/4
Sn=b1*(q^n-1)/(q-1)
S7=81/4 * ((2/3)^7-1) / (2/3 - 1) = 81/4 * (2^7/3^7 - 1) / (-1/3) = 3^4/2^2 * (2^7/3^7-1) * (-3) = -3^5/2^2 * 2^7/3^7 + 3^5/2^2 = 3^5/2^2 - (3^5*2^7)/(2^2*3^7)=243/4-32/9=(243*9-32*4)/(9*4)=2059/36.