{6, 10} и {5, 6, 7, 10, 17}, {5, 6, 10} и {6, 7, 10, 17}; 8 решений.
Пошаговое объяснение:
1) Объединение двух множеств - множество из элементов, принадлежащих хотя бы одному из множеств.
Пересечение - множество элементов, принадлежащих каждому из множеств.
Примеры множеств написаны в ответе.
2) 6 и 10 должны быть в обоих множествах.
Каждое из чисел 5, 7 и 17 должно входить в какое-то из множеств (чтобы попасть в объединение), но только в одно (чтобы не попасть в пересечение).
Для каждого из чисел 5, 7 и 17 есть 2 варианта - попасть в первое или второе множество - и эти варианты можно выбирать независимо. По правилу произведения получится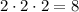 
решений.
Для справки: вот эти решения.
{6, 10} и {5, 6, 7, 10, 17}
{5, 6, 10} и {6, 7, 10, 17}
{6, 7, 10} и {5, 6, 10, 17}
{6, 10, 17} и {5, 6, 7, 10}
{5, 6, 7, 10} и {6, 10, 17}
{5, 6, 10, 17} и {6, 7, 10}
{6, 7, 10, 17} и {5, 6, 10}
{5, 6, 7, 10, 17} и {6, 10}
х:100·20=0,2х м в минуту составляют 20% от х
х-0,2х=0,8х м в минуту - скорость Пятачка
Пусть S - расстояние от домика Винни-Пуха до домика Совы.
S/x минут - время, за которое Винни-Пух доберется до домика Совы.
(S/x):100·20=0,2·(S/x) минут составляют 20% от времени Винни-Пуха.
(S/x)-0,2·(S/x)=0,8·(S/x) минут время Пятачка, которое на 20% меньше времени Винни-Пуха.
С другой стороны, время Пятачка можно найти разделив расстояние от его домика до домика Совы на скорость Пятачка.
(S-360)/(0,8x).
Уравнение
0,8·(S/x) =(S-360)/(0,8x).
Умножим на 0,8х.
0,64S=S-360
0,36S=360
S=1000 метров
О т в е т.
Домик Винни-Пуха находится на расстоянии 1000метров от домика Совы. Домик Пятачка находится на расстоянии 1000-360=640 метров от домика Совы.