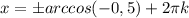Найдите все значения а, при которых уравнение x^3-8=a(x-2) имеет ровно два различных решения

👇

Ответ:

TheEmperorgame

14.02.2022

(x-2)(x²+2x+4)-a(x-2)=0
(x-2)(x²+2x+4-a)=0
x-2=0
x=2
x²+2x+(4-a)=0
D=4-4(4-a)=4-16+4a=4a-12=0
4a=12
a=3
x=-1
ответ при а=3 уравнение имеет 2 различных корня:х=2 и х=-1

4,8(16 оценок)

Открыть все ответы

Ответ:

leralerav

14.02.2022

2cos²x-1=cosx
2cos²x-cosx-1=0
пусть cosx=a, |a|≤1
2a²-a-1=0
D=(-1)²-4*2*(-1)=1+8=9
a₁=(1-3):4=-0,5
a₂=(1+3):4=1
cosx=-0,5
$x=\pm arccos(-0,5)+2\pi k$ ,k∈z
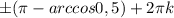x= $\pm ( \pi -arccos0,5)+2 \pi k$ , k∈z
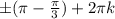x= $\pm (\pi - \frac{\pi}{3}) +2\pi k$ ,k∈z
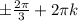x= $\pm \frac{2\pi}{3}+2\pi k$ ,k∈z
корни:
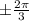если k=0, то x= $\pm \frac{2\pi}{3}$ ,
x=2π/3-является корнем ур-я, а х=-2π/3-не является.
0<2x-π/3<10π/9
0<2*2π/3-π/3<1 1/9 π
0<4π/3-π/3<1 1/9 π
0<π<1 1/9 π
2pi/3-корень уравнения!
------------------------------------------------------------------------------------------------------
cosx=1
x=2πn,n∈z
корней, удовлетворяющих промежутку (0;1 1/9 π) у этого уравнения нет
------------------------------------------------------------------------------------------------------
ответ: 2п/3

4,4(6 оценок)

Ответ:

Sasha0067890

14.02.2022

А) Допустим, на доске написано 99 чисел из арифметической прогрессии, первый член которой равен 1, а последний - 99 (d=1). Тогда их сумма будет равна:
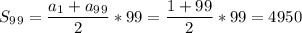
$S_9_9= \dfrac{a_1+a_9_9}{2}*99= \dfrac{1+99}{2}*99=4950$
Это минимально возможная сумма 99 различных натуральных чисел. Прибавим к этой сумме искомое число - 240, получим: 4950+240=5190, что больше 5130 ⇒ в этих 100 числах не может быть числа 240.

Б) Опять исследуем арифметическую прогрессию. На этот раз будет 2 разных последовательности: первая, начинающаяся с 1 и заканчивающаяся 15, и вторая - от 17 до 101. Найдём суммы членов этих прогрессий:
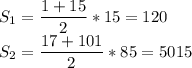
$S_1= \dfrac{1+15}{2}*15=120\\
S_2= \dfrac{17+101}{2}*85=5015\\
$
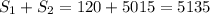S_1+S_2=120+5015=5135

, что больше 5130 ⇒ исключить число 16 не получится.

В) Допустим, что выписаны все числа арифметической прогрессии от 1 до 100 (при d=1). Тогда их сумма будет равна:
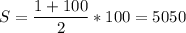$S= \dfrac{1+100}{2}*100=5050$ , что меньше суммы, данной в условии (5130). Так как нас просят найти минимальное количество чисел, кратных 16 (в нашей последовательности это 16, 32, 48, 64, 80 и 96), попробуем заменять их на другие числа, следующие за сотней. Выгоднее будет начинать замену с больших чисел.
Попробуем вычеркнуть 48, 64, 80 и 96. Тогда оставшаяся сумма будет равна 5050-48-64-80-96=4762. Теперь постараемся заменить эти 4 числа минимально возможными, следующими за сотней: 4762+101+102+103+104=5172, что больше 5130. Значит вычеркнуть 4 числа, кратных 16, не получится.
Попробуем вычеркнуть 3 наибольших числа: 5050-64-80-96=4810. 4810+101+102+103=5116, что меньше 5130, значит мы можем заменить, например, число 103 на число 114 и получить в сумме 5130 ⇒ минимально возможное количество цифр кратных 16 в этих 100 числах равно 3.

4,6(17 оценок)

Это интересно:

Стиль-и-уход-за-собой

11.09.2021

Как распутать парик: лучшие советы от профессионалов...

Стиль-и-уход-за-собой

25.09.2020

Как выглядеть великолепно голым: советы от профессионалов...

Компьютеры-и-электроника

12.05.2020

Как копировать музыку, изображения и фильмы на свой компьютер с устройства iPhone...

Финансы-и-бизнес