a) наибольшее 36 и наименьшее 9
б) наибольшее 49 и наименьшее 1
в) наибольшее 81 и наименьшее 0
г) наибольшее 100 и наименьшее 0
Пошаговое объяснение:
Парабола y=x² на интервале (-∞;0) строго убывает, а на интервале (0;+∞) строго возрастает. Поэтому на промежутках содержащих значение х=0 наименьшее значение функции всегда 0, а наибольшее значение функции определяется в граничных точках.
В промежутках не содержащих значение х=0 наибольшее и наименьшее значения функции определяется в граничных точках.
а) [3; 6] не содержит х=0, поэтому наибольшее и наименьшее значения функции определяется среди y(3)=3²=9 и y(6)=6²=36
б) [-7; -1] не содержит х=0, поэтому наибольшее и наименьшее значения функции определяется среди y(-7)=(-7)²=49 и y(-1)=(-1)²=1
в) [-2; 9] содержит х=0, поэтому наибольшее значение функции определяется среди y(-2)=(-2)²=4 и y(9)=9²=81, а и наименьшее значение функции равно 0
г) [-10; 4] содержит х=0, поэтому наибольшее значение функции определяется среди y(-10)=(-10)²=100 и y(4)=4²=16, а и наименьшее значение функции равно 0
Пошаговое объяснение:
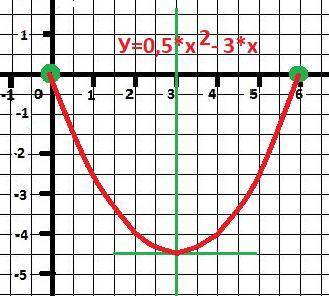
Дано: y =0,5*x²+-3*x+0 - квадратное уравнение.
Положительная парабола - ветви вверх.
Пошаговое объяснение: a*x² + b*x + c = 0 Вычисляем дискриминант - D.
D = b² - 4*a*c = -3² - 4*(0,5)*(0) = 9 - дискриминант. √D = 3.
Вычисляем корни уравнения.
x₁ = (-b+√D)/(2*a) = (3+3)/(2*0,5) = 6/1 = 6 - первый корень
x₂ = (-b-√D)/(2*a) = (3-3)/(2*0,5) = 0/1 = 0 - второй корень
6 и 0 - корни уравнения - точки пересечения с осью ОХ.
Минимальное значение по середине корней при Х=3
У(3) = 1/2*9 - 3*3 = 4.5 * 9 = - 4.5
Таблица с точками для построения графика - в приложении.
Рисунок с графиком в приложении.