с1.
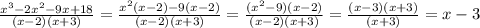
с2.
т.к. лодка была в пути с 8-00 до 20-00, при этом останавливалась на 2 часа, то в движении она пребывала всего 12-2=10 часов.
Пусть скорость лодки х км/ч . Тогда скорость лодки по течению (х+2)км/ч, а против течения (х-2)км/ч. Тогда из А в Б она ехала 15:(x+2) часа, а из Б в А 15:(х-2) часа.
Получаем, что всего в движении лодка была:
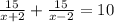
Решаем:
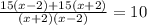
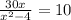
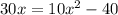
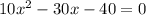
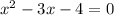
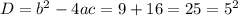
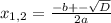
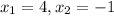
второй корень не подходит, т.к. скорость не может быть отриательной.
ответ: скорость лодки 4км/ч.
с3.
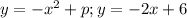
графиком первой функции будет парабола. Графиком второй функции будет прямая.
Т.к. в условии сказано, что у них только одна общая точка, то значит что прямая является касательной к параболе (т.к. если это не касательная, то она пересекет обе ветви параболы).
Т.к. прямая является касательной к параболе, то должно выполнятся условие:
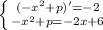
решаем систему уравниений, из которой находим х (одна из координат точки касания) и р.
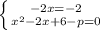
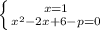
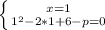
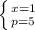
получаем уравнение параболы 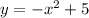
подставляя значение x в любое из уравнений, находим у:
у=-2*1+6
у=4
Т.о. точка касания имеет координаты (1$4)
График во вложении
с4.
Дано: треуг ABC
уголС=90град
BC=24
AC=10
Найти: R
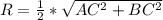
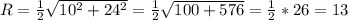
ответ:радиус описанной окружности - 13.
с5.
Дано: ABCD - равнобокая трапеция (AB=CD)
M - равноудалена от B и С
Доказать: AM=MD
Док-во:
BM=CM - т.к. М равноудалена от B и С. Отсюда получаем, что треуг MBC - равнобедренный, а значи угол МВС=уголМСВ
т.к. трапеция равноб., то уголВ=уголС
уголВ= уголМВС + угол МВА
уголС= уголМСВ + угол МCD= угол МВС + угол МCD
Получаем, что угол МCD = угол МВА.
Т.о. треугАВМ=треугMCD - по двум сторонам и углу между ними
Отсюда следует, что AM=MD
рисунок во вложении
с1.
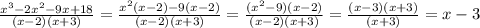
с2.
т.к. лодка была в пути с 8-00 до 20-00, при этом останавливалась на 2 часа, то в движении она пребывала всего 12-2=10 часов.
Пусть скорость лодки х км/ч . Тогда скорость лодки по течению (х+2)км/ч, а против течения (х-2)км/ч. Тогда из А в Б она ехала 15:(x+2) часа, а из Б в А 15:(х-2) часа.
Получаем, что всего в движении лодка была:
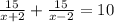
Решаем:
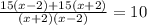
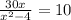
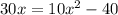
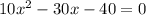
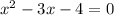
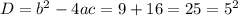
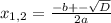
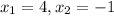
второй корень не подходит, т.к. скорость не может быть отриательной.
ответ: скорость лодки 4км/ч.
с3.
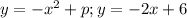
графиком первой функции будет парабола. Графиком второй функции будет прямая.
Т.к. в условии сказано, что у них только одна общая точка, то значит что прямая является касательной к параболе (т.к. если это не касательная, то она пересекет обе ветви параболы).
Т.к. прямая является касательной к параболе, то должно выполнятся условие:
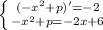
решаем систему уравниений, из которой находим х (одна из координат точки касания) и р.
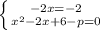
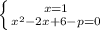
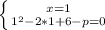
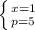
получаем уравнение параболы 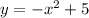
подставляя значение x в любое из уравнений, находим у:
у=-2*1+6
у=4
Т.о. точка касания имеет координаты (1$4)
График во вложении
с4.
Дано: треуг ABC
уголС=90град
BC=24
AC=10
Найти: R
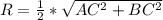
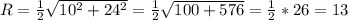
ответ:радиус описанной окружности - 13.
с5.
Дано: ABCD - равнобокая трапеция (AB=CD)
M - равноудалена от B и С
Доказать: AM=MD
Док-во:
BM=CM - т.к. М равноудалена от B и С. Отсюда получаем, что треуг MBC - равнобедренный, а значи угол МВС=уголМСВ
т.к. трапеция равноб., то уголВ=уголС
уголВ= уголМВС + угол МВА
уголС= уголМСВ + угол МCD= угол МВС + угол МCD
Получаем, что угол МCD = угол МВА.
Т.о. треугАВМ=треугMCD - по двум сторонам и углу между ними
Отсюда следует, что AM=MD
рисунок во вложении
Неравенство вида
Решаем первое неравенство:
Решением являются интервалы, расположенные левее меньшего и правее большего корня, так как решается неравенство >0, а парабола направлена ветвями вверх:
Решаем второе неравенство:
Решением является интервал, расположенный между корнями, так как решается неравенство <0, а парабола направлена ветвями вверх:
Тогда, получим систему:
Так как решение системы должно удовлетворять обоим условиям, а интервал
Сравним числа
Значит,
Так как неравенство строгое, то число 5 не входит в решение, а значит наибольшее целое решение неравенства - число 4.
ответы:
решение неравенства:
наибольшее целое решение: число 4