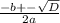. Например: х²-9х+8=0, D=(-9)²-4*1*8, D=81-32, D=49, x1=(9-√49)/2=(9-7)/2=2/2=1, x2=(9+√49)/2=(9+7)/2=16/2=8. Также есть неполные квадратные уравнения (без переменной с), решаются они выносом общего множителя за скобки. Например: 3х-х²=0, х(3-х)=0, х1=0, 3-х=0, х2=3; 3х²+х=0, х(3х+1)=0, х1=0, 3х+1=0, 3х=-1, х=-1/3; 4х²+20х=0, 4х(х+5)=0, 4х=0, х1=0, х+5=0, х=-5.
Пошаговое объяснение:
Движение в противоположных направлении.
Выехал велосипедист и вышел пешеход из одного поселка одновременно.
Скорость велосипедиста 16 км/ч.
Скорость пешехода 4 км/ч.
Время движения 3 ч.
Определить расстояние между ними.
Определим расстояние, которое проехал велосипедист и пешеход по формуле:
S = v * t, где
S — пройденный путь (км),
v — скорость движения (км/ч),
t — время (ч), за которое пройден путь S.
Расстояние, которое проехал велосипедист за 3 часа:
S1 = 16 * 3 = 48 км.
Расстояние, которое пешеход за 3 часа:
S2 = 4 * 3 = 12 км.
Согласно условию задачи, что велосипедист и пешеход вышли одновременно с одного поселка и разных направлениях, то можем определить расстояние между ним после 3 часов движения:
S3 = S1 + S2, км
S3 = 48 + 12 = 60 км.
ответ: расстояние между велосипедистом и пешеходом после 3 часов движения будет 60 км.
a/b+b/b=c/d+d/d;
a/b+1=c/d+1;
a/b=c/d;
b/(a -b) = d/(c-d).
b(c-d)=d(a-b);
(c-d)/d=(a-b)/b;
c/d-d/d=a/b-b/b;
c/d-1=a/b-1;
c/d=a/b;
(a+b)/(a -b) = (c+d)/(c-d);
(a+b)(c-d)=(c+d)(a-b);
ac-ad+bc-bd=ac-bc+ad-bd;
2bc=2ad;
c/d=a/b;