Сократите дробь на наибольший общий делитель ее числителя и знаминателя: 39/130,нод(39,130)=,64/144,нод(64,144)=

👇

Ответ:

Никаgyvhbbuh

25.11.2020

39 = 3 * 13
130 = 2 * 5 * 13
НОД (39 и 130) = 13 - наибольший общий делитель
39/130 = (39:13)/(130:13) = 3/10

64 = 2 * 2 * 2 * 2 * 2 * 2
144 = 2 * 2 * 2 * 2 * 3 * 3
НОД (64 и 144) = 2 * 2 * 2 * 2 = 16 - наибольший общий делитель
64/144 = (64:16)/(144:16) = 4/9

4,6(61 оценок)

Открыть все ответы

Ответ:

мика0955

25.11.2020

Пошаговое объяснение:

При решении задач на нахождение двух чисел по их сумме и разности схематические рисунки. Рассмотрим задачу. В одной корзине на восемь яблок больше, чем во второй. В двух корзинах вместе двадцать яблок. Сколько яблок в каждой корзине? Решение: выполним схематический рисунок. Покажем две корзины, в первой – на восемь яблок больше. Общее количество яблок двадцать. ... ответ: 988 см2. Опираясь на данные задачи, мы можем составить примерную схему решения задач на нахождение двух чисел по их сумме и разности: составляем схему по условию задачи; вычитаем из общей суммы лишнее (уравниваем количество); делим это количество поровну; отвечаем на вопрос задачи

4,5(37 оценок)

Ответ:

soos4

25.11.2020

Во первых рассмотрим функцию:
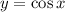
$y=\cos x$

Что бы получить нужную нам функцию, нужно ее растянуть вдоль оси y в два раза.
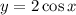
$y=2\cos x$

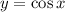При этом, свойства у нее почти одинаковы со свойствами $y=\cos x$ . Отличается лишь область значений.

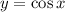У $y=\cos x$ область значений следующая:
$E(\cos x)=[-1,1]$
То есть:
$-1 \leq \cos x \leq 1$
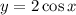Умножаем на два, и получаем область значений $y=2\cos x$ :
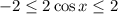
$-2 \leq 2\cos x \leq 2$
Т.е.:
E(y)=[-2,2]

Остальные свойства те же :
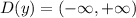$D(y)=(-\infty,+\infty)$ - область определения
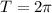$T=2\pi$ - период функции (все тригонометрические функции периодичны) .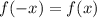

Функция чётна, так как выполняется:
f(-x)=f(x)

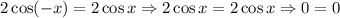$2\cos (-x)=2\cos x \Rightarrow 2\cos x=2\cos x \Rightarrow 0=0$ - тождество.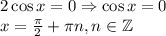

Нули функции:
$2\cos x=0 \Rightarrow \cos x =0\\x= \frac{\pi}{2} +\pi n ,n\in \mathbb Z$

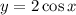Так как $y=\cos x$ достигает экстремумы на концах отрезка области значения, то и $y=2\cos x$ достигает экстремумы на концах отрезка:
[-2,2]

Решаем :
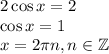$2\cos x=2 \\\cos x=1\\x=2\pi n ,n\in \mathbb Z$ - максимумы.
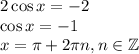$2\cos x=-2 \\\cos x=-1 \\x=\pi +2\pi n,n\in \mathbb Z$ - минимумы.

Положительные значения на интервале $(- \frac{\pi}{2}, \frac{ \pi }{2} )$ и на интервалах, получаемые сдвигом этого интервала на
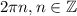
$2\pi n ,n\in \mathbb Z$
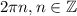
Отрицательные значения на интервале $( \frac{\pi}{2} , \frac{3\pi}{2})$ и на интервалах, получаемые сдвигом этого интервала на $2\pi n ,n\in \mathbb Z$

Функция возрастает на отрезке:
$[\pi,2\pi]$ и на отрезках, получаемых сдвигами этого отрезка на
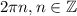
$2\pi n ,n\in \mathbb Z$
Функция убывает на отрезке:
$[0,\pi]$ и на отрезках, получаемых сдвигами этого отрезка на
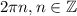
$2\pi n ,n\in \mathbb Z$

Y=2cosx построить график функции и описать его свойства пож решитее