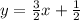или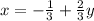 
Пошаговое объяснение:
Нам нужно составить уравнение геометрического места точек на плоскости ОXY равноудаленных от точек с координатами A (2; -3) и B (-4; 1).
Решать задачу будем следующим образом:
вспомним формулу для нахождения расстояния между точками на плоскости;
обозначим точки равноудаленные от А и В координатами (x; y);
запишем расстояния между точкой А и (x; y);
запишем расстояние между точками B и (x; y);
приравняем расстояния и выразим одну переменную через другую.
Вспомним формулу для нахождения расстояния на плоскости
Формула для нахождения расстояния между точками на плоскости выглядит так:
AB =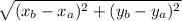 
, где точки А и В заданы координатами A и B
Формулу мы вспомнили, теперь можем записать расстояние между точками А с координатами (2; -3) и (x; y) и точками B с координатами (-4; 1) и (x; y).
Составим уравнение геометрического места точек
Записываем расстояние между точкой A (2; -3) и (x; y):
;
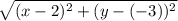Записываем расстояние между точками B (-4; 1) и (x; y):
;
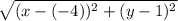Так как геометрического места точек на плоскости ОXY равноудаленных от точек A и B мы приравниваем полученные выражения:
;
;
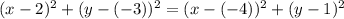Открываем скобки, переносим все слагаемые в право и приводим подобные.
;
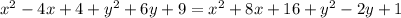
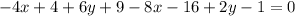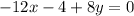
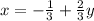
или
.
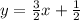2) 1 7/20 + 1 16/20 = 2 23/20 = 3 3/20 ( кг ) в первом и втором
3) 5 - 3 3/20 = 4 20/20 - 3 3/20 = 1 17/20 ( кг ) в третьем
ответ 1 17/20 кг ( или 1,85 кг )