Три закона диалектики.
1. Закон перехода количественных отношений в качественные (при изменении количественных отношений после определенной стадии происходит изменение качества из-за неразрушения меры) .
На бытовом уровне этот закон хорошо иллюстрируется на примере человека, вся жизнь которого состоит из борьбы противоположностей. В каждом человеке сочетаются хорошие и плохие качества. В одной ситуации человек будет вести себя как «человек» , в другой нет; сегодня он один, завтра - другой; окружающая среда постоянно меняет человека, но и он постоянно ее меняет
2. Закон направления развития (отрицание отрицания) . Голое отрицание - нечто идущее после данного объекта, полностью его уничтожающее. Диалектическое отрицание: сохраняется нечто от первого объекта - воспроизведение этого объекта, но в другом качестве. Вода - лед. Смолотить зерно - голое отрицание, посадить зерно - диалектическое отрицание. Развитие происходи по спирали.
Один человек, например, подчиняется одним законам, а вот толпа существует по несколько иным законам. Момент перехода из одного качественного состояния в другой называется скачок. Он может быть эволюционным или революционным.
3. Закон единства и борьбы противоположностей. Противоречие между формой и содержанием, возможностью и реальностью. Причина развития - единство и борьба противоположностей. Это присуще духу. Изначально тождество, но потенциально таит различие. Тождество - различие - противоположность. Противоположности взаимодействуют, то есть борются.
Смысл этого закона можно легко понять на следующем примере. Маркс (создатель современной материалистической диалектики) , отрицал идеалистическую диалектику Гегеля. Но диалектика Маркса вряд ли бы появилась без диалектики Гегеля.
122, 123, 125, 129, 133, 134, 141, 142, 143
Пошаговое объяснение:
Если разложение на простые множители числа N имеет вид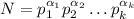 
, то у него ровно 
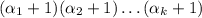делителей: в самом деле, все делители получатся, если в разложении независимо менять показатели степеней на 0, 1, 2, ..., α.
Применив это, получаем, что нужно найти все числа, имеющие вид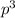 
или pq, где p, q - различные простые числа.
С кубами всё просто - в рассматриваемый промежуток попадает только 125.
Разбираемся с остальными, уже выкинуты 125 и 121 - квадрат 11:
121, 122, 123, 124, 125, 126, 127, 128, 129, 130, 131, 132, 133, 134, 135, 136, 137, 138, 139, 140, 141, 142, 143, 144
Выкидываем простые:
121, 122, 123, 124, 125, 126, 127, 128, 129, 130, 131, 132, 133, 134, 135, 136, 137, 138, 139, 140, 141, 142, 143, 144
Выкидываем делящиеся на 4:
121, 122, 123, 124, 125, 126, 127, 128, 129, 130, 131, 132, 133, 134, 135, 136, 137, 138, 139, 140, 141, 142, 143, 144
Выкидываем делящиеся на 9:
121, 122, 123, 124, 125, 126, 127, 128, 129, 130, 131, 132, 133, 134, 135, 136, 137, 138, 139, 140, 141, 142, 143, 144
Остальные можно проверить непосредственно, отсеются 130 = 2 * 5 * 13 и 138 = 2 * 3 * 23.
