вот
Пошаговое объяснение: y'' + 10y' + 24y = 6e^(-6x) + 168x + 118
Неоднородное уравнение 2 порядка.
y(x) = y0 + y* (решение однородного + частное решение неоднородного).
Решаем однородное уравнение
y'' + 10y' + 24y = 0
Характеристическое уравнение
k^2 + 10k + 24 = 0
(k + 4)(k + 6) = 0
y0 = C1*e^(-4x) + C2*e^(-6x)
Находим частное решение неоднородного уравнения
-6 - один из корней характеристического уравнения, поэтому
y* = A*x*e^(-6x) + B1*x + B2
y* ' = A*e^(-6x) - 6Ax*e^(-6x) + B1
y* '' = -6A*e^(-6x) - 6A*e^(-6x) + 36A*x*e^(-6x)
Подставляем в уравнение
-6A*e^(-6x) - 6A*e^(-6x) + 36A*x*e^(-6x) + 10A*e^(-6x) - 60Ax*e^(-6x) + 10B1 + 24A*x*e^(-6x) + 24B1*x + 24B2 = 6e^(-6x) + 168x + 118
(-6A - 6A + 36A*x + 10A - 60A*x + 24A*x)*e^(-6x) + 24B1*x + (10B1 + 24B2) =
= 6e^(-6x) + 168x + 118
Приводим подобные в скобке при e^(-6x)
-12A + 10A + 60A*x - 60A*x = -2A
Подставляем
-2A*e^(-6x) + 24B1*x + (10B1 + 24B2) = 6e^(-6x) + 168x + 118
Коэффициенты при одинаковых множителях должны быть равны
{ -2A = 6
{ 24B1 = 168
{ 10B1 + 24B2 = 118
Решаем
{ A = -3
{ B1 = 7
{ 70 + 24B2 = 118; B2 = (118 - 70)/24 = 48/24 = 2
y* = -3x*e^(-6x) + 7x + 2
ответ: y = y0 + y* = C1*e^(-4x) + C2*e^(-6x) - 3x*e^(-6x) + 7x + 2
Дано
Площадь одной плитки = 400:
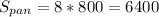
Найти к-во Q потребующихся для замощения панели плиток
Решение
Нужно разделить пл. всей панели на пл. 1 плитки:
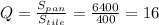
ответ 16
Задача 2Дано
Периметр прямоугольника (Prec) = 120. У прямоугольника противоположные стороны равны. Сторона a = b + 10 Сторона b = x (тогда a = x + 10)Найти площадь прямоугольника Srec
Решение
Исходя из формулы нахождения P прямоугольника, имеем
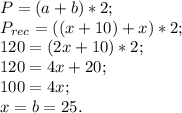
Мы нашли длину стороны b. Отсюда находим сторону a:
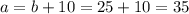
Площадь прямоугольника Srec является произведением длин его сторон:
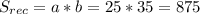
ответ 875 кв. см
Задача 3Купил тетрадей на сумму 8 (шт) * 25 (тг) = 200 (тг),купил ручек на сумму 3 (шт) * 120 (тг) = 360 (тг).ответ: всего потратил 200 + 360 = 560 тг.
Задача 4Дано
Прямоугольник j,его сторона a = 7,его периметр P = 40Найти сторону b
По формуле периметра прямоугольника получаем формулу для нахождения стороны b:
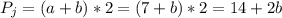
Периметр известен, подставляем его значение в формулу и находим b:
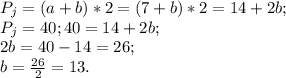
ответ 13
Задача 5Дано
Квадрат с периметром 36 см
Найти его площадь
Решение
Площадь квадрата – это, как бы неловко ни звучало, квадрат его одной стороны.
Введём переменную для стороны квадрата – a. Зная, что стороны квадрата равны, а их 4, работаем с первой известной нам из "Дано" переменной – с периметром. По формуле нахождения периметра квадрата получаем, что сторона a = 9:
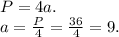
Второй и последний шаг – площадь квадрата. Значения всех необходимых переменных нам теперь известны (сторона):
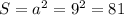
ответ 81 кв. см