ответ: x = ± 5.
Дано: x⁴ - 10*x³ + 250*x - 625 = 0.
Пошаговое объяснение:
Применим теорему Безу, по которой свободный член полинома = -625 - произведение корней уравнения.
Эта теорема выглядит так.
x₁ * x₂ * x₃ * x₄ = - 625 = - 5⁴
Можно предположить, что два корня действительные: +/- 5.
(x -5) * (x+ 5) * (х -x₃) * (х- x₄) = 0
Проверим это делением многочленов - разделим сразу на : (х² - 25)
Расчет на рисунке в приложении.
Разделилось без остатка и получили в результате
x² - 10*x + 25 = (х - 5)² = 0
Решаем это квадратное уравнение и получаем еще два корня: х = 5
Должно получиться: (x-5)³*(x+5) = 0.
В подтверждение расчёта - график функции - в приложении.
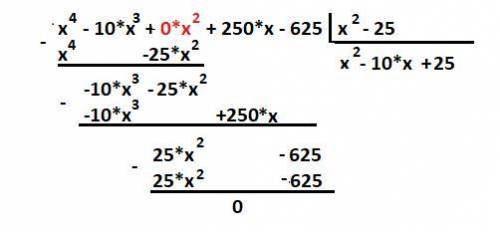
90-36:3*2=66
84:4*3+2=65
100-10*9-8=2
17+15*3*0=17
5*5+75:5=40
17*3+2*10=71
80-5*2:10=79
72:6+6*5=42