Пошаговое объяснение:
Диагональ прямоугольника равна по теореме Пифагора :
sqrt ( 6^2+ 8^2) =10( см). В прямоугольном треугольнике с высотой пирамиды гипотенуза равна 13 см, один из катетов - 5см ( половина диагонали прямоугольника). Высота по теореме Пифагора равна sqrt(13^2 - 5^2)=12(см). Площадь полной поверхности складывается из площади основания, площадей двух пар равных боковых граней. Площадь основания равна 6х8=48 (кв. см). Апофемы ( высоты боковых граней ) находятся из прямоугольных треугольников с высотами пирамиды. Вторые катеты равны половине сторон основания. Т.о. одна апофема по теореме Пифагора равна sqrt (12^2 + 4^2)=4 sqrt 10. Другая апофема равна sqrt(12^2 +3^2)=sqrt 153. Площадь боковой грани с первой апофемой равна 6х4sqrt 10/2=12 sqrt 10. Площадь боковой грани со второй апофемой равна 8хsqrt 153 /2= 4 sqrt 153. И площадь полной поверхности пирамиды равна ( 48 + 24 sqrt 10+ 8 sqrt 153) кв. см.
2 задача. 2 боковые ребра находятся из прямоугольных треугольников, содержащих высоту пирамиды, а второй катет - половина известной диагонали (6:2=3). Мы получаем египетский треугольник : катеты равны 4 см и 3 см , поэтому боковое ребро = 5 см. Чтобы найти оставшиеся боковые рёбра, надо
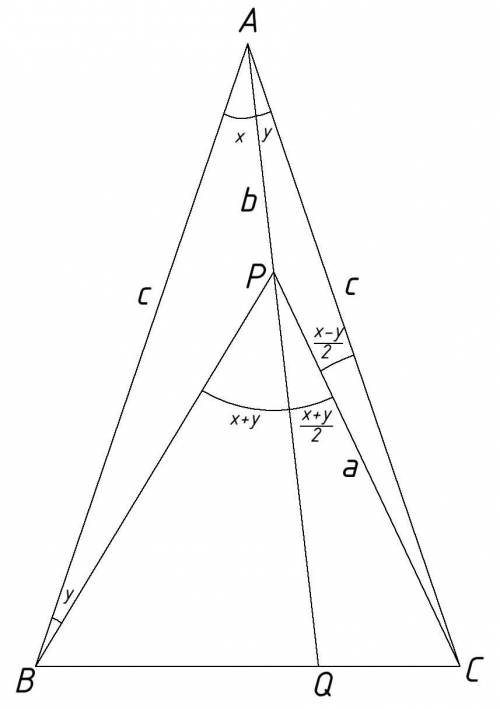
Все обозначения смотри на рисунке.
Из рассуждений суммы углов треугольника и смежных углов получаем что:
∠BPQ=x+y
∠QPC=(x+y)/2
По тем же рассуждениям можно получить,что:
∠PCA=(x-y)/2
Так же сразу отметим что:
∠CPA=180-(x+y)/2 → sin∠CPA=sin(180-(x+y)/2)=sin ( (x+y)/2 )
∠BPA=180-(x+y) → sin∠BPA=sin(x+y)
Это пригодится нам в дальнейшем.
Очевидно, что площади треугольников:
SΔBAQ/SΔQAC=BQ/QC ,тк они имеют общую высоту.
Тогда:
1/2 *c*b*sin(x)/ (1/2 *c*b*sin(y) )=BQ/QC
sin(x)/sin(y)=BQ/QC
Запишем теоремы синусов для ΔBAP и ΔPAC:
1)c/sin(x+y)=b/sin(y)
2)c/sin( (x+y)/2)=a/sin(y)
3) a/sin(y)=b/sin(x-y)/2 → a/b=sin(y)/sin ((x-y)/2)
Поделим 2) на 1)
sin(x+y)/sin ( (x+y)/2)=a/b
Откуда:
sin(x+y)/sin ( (x+y)/2)=sin(y)/sin ((x-y)/2)
2*sin( (x+y)/2 )*cos( (x+y)/2) /sin( (x+y)/2)=sin(y)/sin ((x-y)/2)
2*cos( (x+y)/2)=sin(y)/sin( (x-y)/2)
2*cos( (x+y)/2) * sin( (x-y)/2)=sin(y)
Применяем формулу произведения синуса на косинус:
2*1/2 *( sin( (x+y)/2 + (x-y)/2 ) +sin( (x-y)/2 -(x+y)/2 ) )=sin(y)
sin(x)-sin(y)=sin(y)
sin(x)=2*sin(y)
sin(x)/sin(y)=2
BQ/QC=sin(x)/sin(y)=2
Таким образом:
BQ=2*QC
ЧТД.
2)40:8=5 шт это на 40руб
3) 58÷8=7,25 т.е 7 шт на 58 рублей .