Начертите окружность .отметьте на окружности точки a,b,c,d.проведите отрезки ab,ac,ad.как долженпроходить отрезок ,соеденяющий две точки одной окружности,чтобы имел наибольшую длину? сделайте вывод: отрезок,соединяющий две точки одной окружности,имеет наибольшую длину,

👇

Увидеть ответ

Ответ:

leha2018

14.09.2021

Отрезок, соединяющий две точки одной окружности имеет наибольшую длину, если он проходит через центр данной окружности.

Этот отрезок прямой называется диаметром окружности.

На приложенном рисунке, диаметром окружности является отрезок АВ.

[AB] = 10 cm

[AD] = 9.8 cm

AC] = 9.5 cm

Можно сделать вывод, что, чем ближе орезок, соединяющий 2 точки, лежащие на окружности, к пересечению с центром окружности, тем он длиннее.

Начертите окружность .отметьте на окружности точки a,b,c,d.проведите отрезки ab,ac,ad.как долженпрох

4,5(10 оценок)

Открыть все ответы

Ответ:

shumskaya03

14.09.2021

Созданный российским скульптором Алексеем Леоновым бронзовый памятник первому космонавту установили в парке у исторического здания штаб-квартиры NASA в техасском Хьюстоне.

В церемонии приняли участие директор космического ведомства Чарльз Болден, мэр Хьюстона Анис Паркер, представители американских общественных организаций и научно-исследовательских учреждений, МИД России и организаций российских соотечественников.

Среди почетных гостей — дочь и внук Юрия Гагарина Галина и Юрий, президент финансировавшего работы по созданию монумента международного благотворительного фонда «Диалог культур — единый мир» Руслан Байрамов и региональный директор фонда «Русский мир» Николай Михайлов.

На мероприятии была зачитана приветственная телеграмма губернатора Калужской области Анатолия Артамонова. «Это особенно символично, так как история мировой космонавтики начиналась именно из Калуги — города, где жил и работал Константин Циолковский. Связь Калуги с центром американской космонавтики, которым является Хьюстон, однозначна. Памятник Юрию Гагарину — российский подарок Хьюстону — является дополнительным подтверждением растущего взаимодействия между Россией и США в освоении Вселенной», — заявил Байрамов.

«Российско-американское сотрудничество в космосе укрепляется. Памятник первому гражданину Земли, которому удалось совершить полет вокруг нашей планеты, подтверждает это и напоминает, что его подвиг интернационален и в равной мере принадлежит всему человечеству», — заверил мэр Хьюстона.

К открытию мемориала приурочено создание Аллеи космонавтов перед зданием Космического центра имени Линдона Джонсона в Хьюстоне. В течение ближайших нескольких недель там планируется посадить 50 деревьев.

4,5(26 оценок)

Ответ:

паша573

14.09.2021

Пошаговое объяснение:

Ромб - параллелограмм у которого все стороны равны .

Теорема : Диагонали ромба пересекаются под прямым углом и лежат на биссектрисах его углов

Доказательство :

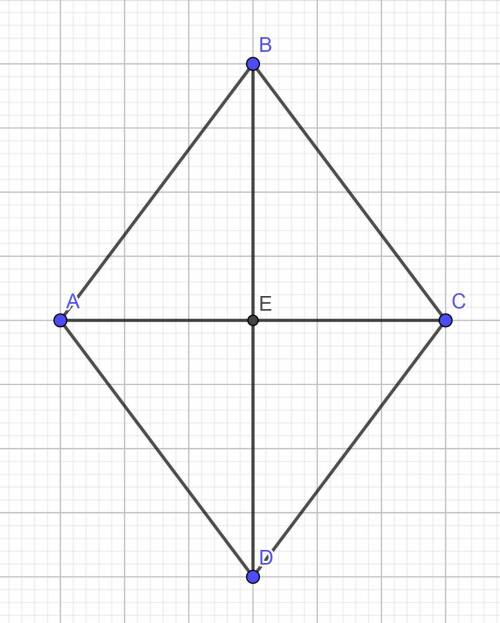
Нарисуем ромб АВСД ( рисунок во вложении ) .Рассмотрим ΔАВD . Поскольку у ромба все стороны равны , то АВ=AD , а это значит , что ΔABD - равнобедренный .Поскольку ромб это параллелограмм , значит диагонали в точке пересечения делятся пополам, т.е. ВЕ=ЕD. По-этому можно утверждать , что АЕ - это медиана (отрезок соединяющий вершину с серединой противоположной стороны) , а по свойству равнобедренного треугольника : медиана, проведенная к основанию, является биссектрисой и высотой, а значит АЕ - высота и биссектриса Δ АВD. Следовательно АЕ⊥BD и угол ВАЕ = углу DAE, что говорит о том , что диагонали ромба пересекаются под прямым углом и лежат на биссектрисах его углов.